Как найти выборочную среднюю
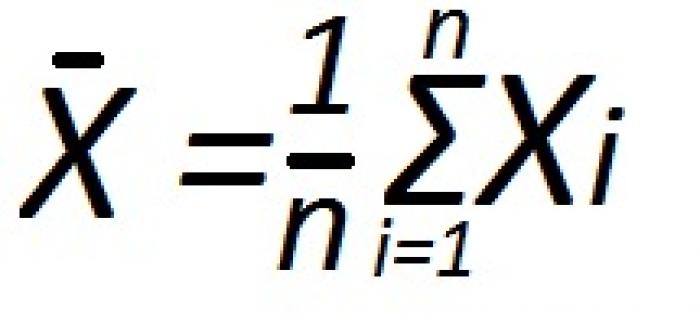
- Выборочная средняя: определение и применение
- Нахождение выборочной средней
- Выборочная средняя и средняя арифметическая
- Заключение
Выборочная средняя: определение и применение
Выборочная средняя - это математическая величина, которая характеризует выборку из n чисел различной величины со стороны ее среднего значения. Это понятие находит широкое применение в математической статистике, теории вероятностей и других областях знания. Давайте разберемся, каким образом находится выборочная средняя и как она отличается от средней арифметической.
Нахождение выборочной средней
Итак, для того чтобы найти выборочную среднюю, необходимо иметь выборку из числовых значений. Предположим, у нас есть совокупность из n единиц. Все эти единицы образуют выборку. Сумма всех чисел в выборке обозначается как ΣXi, где Xi - это одно из значений выборки, а i - это номер значения. Чтобы найти выборочную среднюю, нужно сложить все значения выборки и поделить на их количество n.
Выборочная средняя и средняя арифметическая
В школьной программе формула для нахождения среднего значения уже знакома многим ученикам. Когда в 5 классе на уроке математики просят найти среднее значение каких-либо чисел, дети уже знают, что нужно сложить все числа и поделить на их количество. Фактически они находят выборочную среднюю. Однако с математической точки зрения выборочная средняя рассматривается не как заданная совокупность, а как пространство, в котором существует множество произвольных значений. Исследуя это пространство, находим выборочную совокупность и, в конечном итоге, выборочную среднюю.
Заключение
Выборочная средняя - это важная математическая величина, которая помогает описать выборку из n чисел. Нахождение выборочной средней требует сложения всех значений выборки и их деления на количество. Это понятие находит применение в различных областях знания и помогает проводить анализ данных.