Как найти высоту четырёхугольной призмы
- Что такое призма?
- Как вычислить высоту призмы?
- Формула вычисления высоты призмы
- Вычисление высоты призмы с квадратным или прямоугольным основанием
- Вычисление высоты правильной четырехугольной призмы
- Вычисление высоты призмы с диагональю основания
Что такое призма?
Призмой называют объемную фигуру, составленную из некоторого количества прямоугольных боковых граней и двух параллельных друг другу оснований. Основания могут иметь форму любого многоугольника, включая и четырехугольник.
Как вычислить высоту призмы?
Высотой призмы называют перпендикулярный основаниям отрезок между плоскостями, в которых они лежат. Для вычисления высоты призмы существуют различные формулы в зависимости от известных данных.
Формула вычисления высоты призмы
Если в условиях задачи приведен объем (V) пространства, ограниченного гранями призмы, и площадь ее основания (s), для вычисления высоты (H) используйте формулу, общую для призм с основанием любой геометрической формы. Разделите объем на площадь основания: H=V/s.
Вычисление высоты призмы с квадратным или прямоугольным основанием
Если четырехугольник, лежащий в основании призмы, имеет форму какой-либо правильной фигуры, вместо площади в вычислениях можно использовать длины ребер призмы. Например, при квадратном основании площадь в формуле предыдущего шага замените второй степенью длины его ребра (a): H=V/a². А в случае прямоугольника в ту же формулу подставьте произведение длин двух смежных ребер основания (a и b): H=V/(a*b).
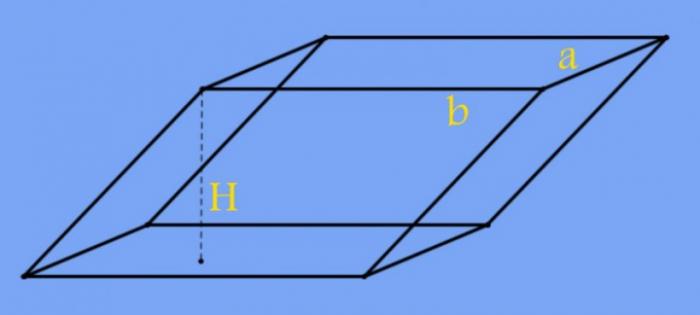
Вычисление высоты правильной четырехугольной призмы
Для вычисления высоты (H) правильной четырехугольной призмы может оказаться достаточным знания полной площади поверхности (S) и длины одного ребра основания (a). Так как общая площадь складывается из площадей двух оснований и четырех боковых граней, а в таком многограннике основанием является квадрат, площадь одной боковой поверхности должна быть равна (S-a²)/4. Эта грань имеет два общих ребра с квадратными основаниями известного размера, значит, для вычисления длины другого ребра разделите полученную площадь на сторону квадрата: (S-a²)/(4*a). Так как рассматриваемая призма является прямоугольной, то ребро вычисленной вами длины примыкает к основаниям под углом 90°, т.е. совпадает с высотой многогранника: H=(S-a²)/(4*a).
Вычисление высоты призмы с диагональю основания
В правильной четырехугольной призме для вычисления высоты (H) достаточно знания длины диагонали (L) и одного ребра основания (a). Рассмотрите треугольник, образуемый этой диагональю, диагональю квадратного основания и одним из боковых ребер. Ребро здесь - неизвестная величина, совпадающая с искомой высотой, а диагональ квадрата, основываясь на теореме Пифагора, равна произведению длины стороны на корень из двойки. В соответствии с той же теоремой выразите искомую величину (катет) через длины диагонали призмы (гипотенузы) и диагонали основания (второй катет): H=√(L²-(a*V2)²)=√(L²-2*a²).
Теперь вы знаете, как вычислить высоту призмы в различных ситуациях. Это позволит вам решать задачи, связанные с измерением объемов и площадей призм.






