Как научиться решать матрицы
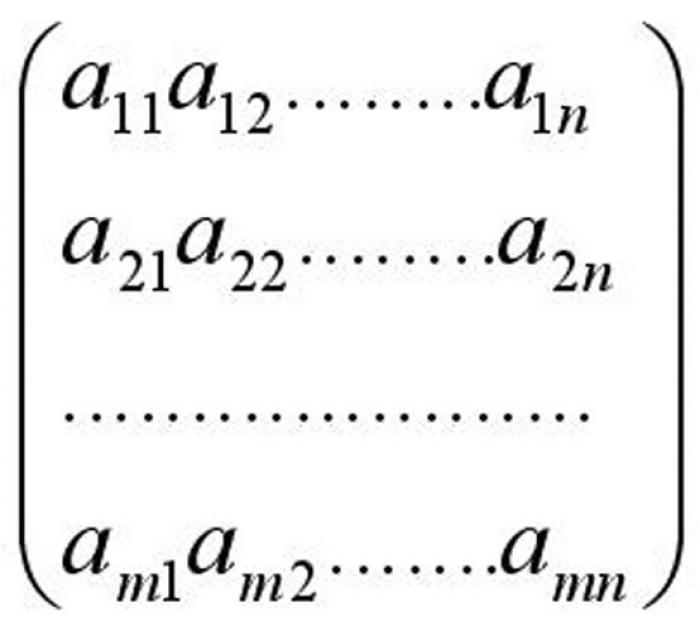
- Матрицы: основные понятия
- Основные понятия матрицы
- Виды матриц
- Симметрия и согласованность матриц
- Основные действия с матрицами
Матрицы: основные понятия
Матрицы, которые на первый взгляд могут показаться непонятными, на самом деле имеют широкое практическое применение в экономике и бухгалтерии. Внешне матрицы выглядят как таблицы, состоящие из чисел, функций или других величин, размещенных в столбцах и строках. Они имеют несколько видов и определенные элементы.
Основные понятия матрицы
Для того чтобы научиться решать матрицы, необходимо познакомиться с ее основными понятиями. Главными элементами матрицы являются ее диагонали - главная и побочная. Главная диагональ начинается с элемента в первом ряду и первом столбце, и продолжается до элемента последнего столбца и последнего ряда (слева направо). Побочная диагональ, напротив, начинается в первом ряду, но последнем столбце, и продолжается до элемента, имеющего координаты первого столбца и последнего ряда (справа налево).
Виды матриц
Для того чтобы перейти к следующим определениям и алгебраическим операциям с матрицами, необходимо изучить их различные виды. Самые простые из них - квадратная, транспонированная, единичная, нулевая и обратная. Квадратная матрица имеет одинаковое количество столбцов и строк. Транспонированная матрица, обозначаемая как В, получается из матрицы А путем замены столбцов на строки. В единичной матрице все элементы главной диагонали равны единице, а остальные элементы равны нулю. В нулевой матрице все элементы, включая элементы диагоналей, равны нулю. Обратная матрица - это такая матрица, которая при умножении на исходную матрицу приводит ее к единичному виду.
Симметрия и согласованность матриц
Матрица может быть симметрична относительно главной или побочной осей. Это означает, что элемент, имеющий координаты (1;2), равен элементу с координатами (2;1). Также матрицы могут быть согласованными, то есть количество столбцов одной матрицы равно количеству строк другой матрицы. Согласованные матрицы можно перемножать.
Основные действия с матрицами
Основные действия, которые можно совершать с матрицами, включают сложение, умножение и нахождение определителя. Если матрицы имеют одинаковый размер, то их можно сложить. При сложении необходимо складывать элементы, стоящие на одинаковых местах в матрицах. При умножении согласованных матриц получается новая матрица, где каждый элемент является суммой попарно перемноженных элементов строки первой матрицы и столбца второй матрицы. Порядок действий очень важен при умножении матриц. Определитель матрицы - это величина, которая определяется по модулю и не может быть отрицательной. Для квадратной матрицы 2х2 детерминант вычисляется путем перемножения элементов главной диагонали и вычитания из них перемноженных элементов побочной диагонали.
Теперь, когда вы знакомы с основными понятиями и действиями с матрицами, их использование в экономике и бухгалтерии станет более понятным и доступным.