Как определить промежутки монотонности
- Определение интервалов монотонности функции
- Шаг 1: Вычисление области определения функции
- Шаг 2: Нахождение границ интервалов монотонности
- Шаг 3: Определение знака производной на полученных интервалах
- Шаг 4: Определение точек экстремума функции
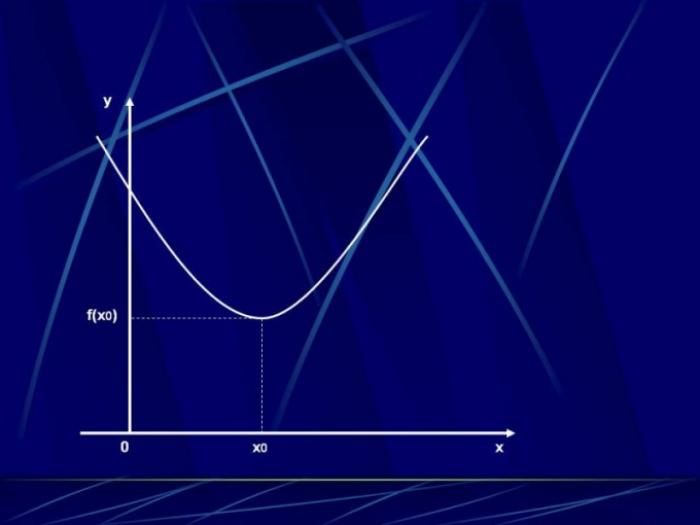
Определение интервалов монотонности функции
Для решения задачи по определению интервалов, в которых функция монотонно возрастает или убывает, необходимо выполнить ряд определенных действий. Это часто требуется в алгебраических задачах.
Шаг 1: Вычисление области определения функции
Первым шагом является вычисление области определения функции. Для этого необходимо определить все значения аргументов, при которых можно найти значение функции. Отметить точки, где наблюдаются разрывы.
Шаг 2: Нахождение границ интервалов монотонности
Точки, в которых функция не существует или ее производная равна нулю, являются границами интервалов монотонности. Эти диапазоны, а также точки, их разделяющие, следует последовательно внести в таблицу.
Шаг 3: Определение знака производной на полученных интервалах
Чтобы определить знак производной функции на полученных интервалах, необходимо в выражение, соответствующее производной, подставить любой аргумент из интервала. Если результат положительный, функция возрастает, в обратном случае - убывает. Результаты заносятся в таблицу.
Шаг 4: Определение точек экстремума функции
В таблицу необходимо внести информацию о точках экстремума функции. Это точки, в которых производная равна нулю. Экстремум может быть точкой максимума или точкой минимума. Если предыдущий участок функции возрастал, а текущий убывает, значит, это точка максимума. В случае, когда до данной точки функция убывала, а теперь возрастает, это точка минимума. Значения функции в точках экстремума также заносятся в таблицу.
Таким образом, выполнение указанных выше шагов позволяет определить интервалы монотонности функции и выявить точки экстремума. Эта информация может быть полезной при решении алгебраических задач.