Как построить график линейной функции
- График линейной функции
- Построение графика линейной функции
- Построение графика функции y = 3 * x + 1
- Частные случаи линейных функций
- Проверка графика и полезные советы
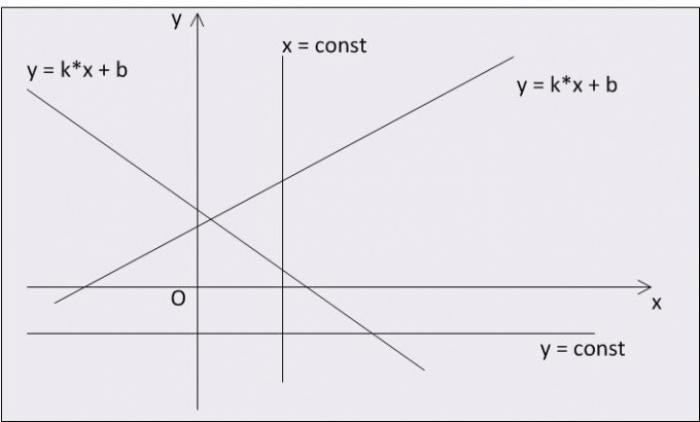
График линейной функции
Линейная функция - это функция, которая может быть представлена уравнением y = k * x + b, где k и b - некоторые числа. Графически она представляется прямой линией на координатной плоскости. Такие функции широко используются в физике и технике для описания зависимостей между различными величинами.
Построение графика линейной функции
Для построения графика линейной функции необходимо знать как минимум две точки на этой прямой. Для удобства и точности построения, можно найти пять точек на заданной функции. Для этого подставляем значения x = -1, 0, 1, 3, 5 в уравнение функции и находим соответствующие значения y.
Построение графика функции y = 3 * x + 1
Для примера рассмотрим функцию y = 3 * x + 1. Подставляя значения x = -1, 0, 1, 3, 5, находим соответствующие значения y: -2, 1, 4, 10, 16. Затем отмечаем эти точки на координатной плоскости и проводим прямую линию через них.
Частные случаи линейных функций
Существуют два распространенных частных случая линейных функций. Первый случай - функция y = const, где значение y постоянно для любого значения x. График такой функции является горизонтальной прямой линией. Второй случай - функция x = const, где значение x всегда постоянное. График такой функции является вертикальной прямой линией.
Проверка графика и полезные советы
При построении графика линейной функции, важно учесть значение коэффициента k. Если k > 0, то прямая будет образовывать острый угол с осью абсцисс, а если k < 0, то прямая будет образовывать тупой угол с осью абсцисс. Также следует помнить, что прямая не должна иметь начала и конца, поэтому ее следует проводить за крайние точки. Если задание требует построения графика на отрезке, то прямую необходимо ограничить требуемыми точками.