Как построить параболоид
- Параболоид: формы и сечения
- Эллиптический параболоид
- Строительство параболоида
- Гиперболический параболоид
- Построение гиперболического параболоида
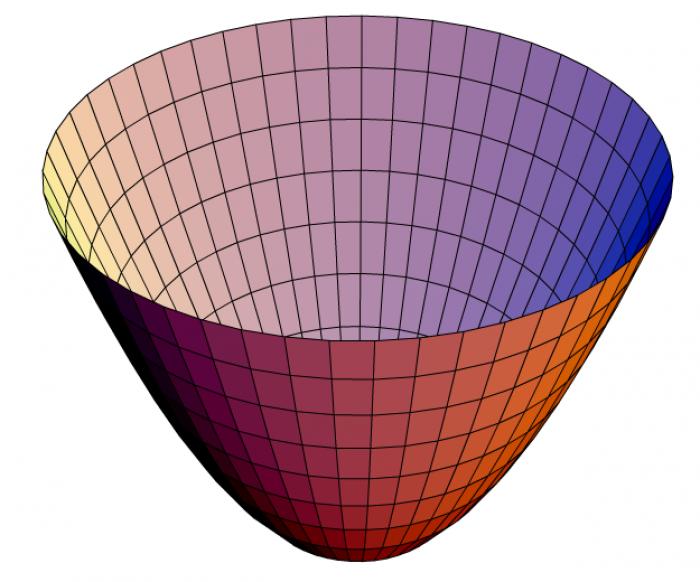
Параболоид: формы и сечения
При вращении параболы вокруг своей оси получается объемная фигура, называемая параболоидом. У параболоида есть несколько сечений, среди которых основное - это парабола, и следующее - это эллипс. При построении учитываются все характеристики графика параболы, от которой зависит форма и вид параболоида.
Эллиптический параболоид
Если повернуть параболу на 360 градусов вокруг своей оси, можно получить обыкновенный эллиптический параболоид. Он представляет собой полое изометрическое тело, сечениями которого являются эллипсы и параболы. Эллиптический параболоид задается уравнением вида: x^2/a^2 + y^2/b^2 = 2z. Все главные сечения параболоида являются параболами. При сечении плоскости XOZ и YOZ получаются только параболы. Если провести перпендикулярное сечение относительно плоскости Xoy, можно получить эллипс. Причем, сечения, представляющие собой параболы, задаются уравнениями вида: x^2/a^2 = 2z; y^2/a^2 = 2z. Сечения эллипса задаются другими уравнениями: x^2/a^2 + y^2/b^2 = 2h. Эллиптический параболоид при a=b превращается в параболоид вращения.
Строительство параболоида
Построение параболоида имеет ряд некоторых особенностей которые нужно учитывать. Операцию начните с подготовки основы - чертежа графика функции. Для того чтобы начать строить параболоид, нужно вначале построить параболу. Начертите параболу в плоскости Oxz, как показано на рисунке. Задайте будущему параболоиду определенную высоту. Для этого проведите прямую таким образом, чтобы она касалась верхних точек параболы и была параллельно оси Ox. Затем начертите параболу в плоскости Yoz и проведите прямую. Вы получите две параболоидные плоскости, перпендикулярные друг другу. После этого в плоскости Xoy постройте параллелограмм, который поможет начертить эллипс. В этот параллелограмм впишите эллипс таким образом, чтобы он касался всех его сторон. После этих преобразований сотрите параллелограмм, и останется объемное изображение параболоида.
Гиперболический параболоид
Существует также гиперболический параболоид, который имеет более вогнутую форму, чем эллиптический. Его сечения также имеют выд параболы, а в некоторых случаях - гиперболы. Главные сечения по Oxz и Oyz, как и у эллиптического параболоида, представляют собой параболы. Они задаются уравнениями вида: x^2/a^2 = 2z; y^2/a^2 = -2z. Если провести сечение относительно оси Oxy, можно получить гиперболу. При построении гиперболического параболоида руководствуйтесь следующим уравнением: x^2/a^2 - y^2/b^2 = 2z - уравнение гиперболического параболоида.
Построение гиперболического параболоида
Первоначально постройте неподвижную параболу в плоскости Oxz. В плоскости Oyz начертите подвижную параболу. После этого задайте высоту параболоида h. Для этого отметьте на неподвижной параболе две точки, которые будут вершинами еще двух подвижных парабол. Затем изобразите еще одну систему координат O'x'y', чтобы нанести гиперболы. Центр этой системы координат должен совпадать с высотой параболоида. После всех построений изобразите те две подвижные параболы, о которых упоминалось выше, так чтобы они касались крайних точек гипербол. В результате получится гиперболический параболоид.