Как рассчитать высоту правильной пирамиды

- Нахождение высоты пирамиды с квадратным основанием
- Формула для нахождения высоты пирамиды с квадратным основанием
- где [(1-cos^2α)/cos^2α = tg^2α].
- Нахождение высоты пирамиды с треугольным основанием
- Формула для нахождения высоты пирамиды с треугольным основанием
- H = a*tgα/√3
- h = √5+2√5a/2
- k/cosα = √5+2√5a/4cosα
- H = √[(√5+2√5a/4cosα)^2 - (√5+2√5a/4)^2]
Нахождение высоты пирамиды с квадратным основанием
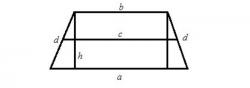
Для определения высоты пирамиды с квадратным основанием необходимо провести высоту, перпендикулярную плоскости основания. В результате получится прямоугольный треугольник, где гипотенуза является ребром пирамиды, а больший катет - ее высотой. Меньший катет проходит через диагональ квадрата и численно равен ее половине. Если известен угол между ребром и плоскостью основания, а также одна из сторон квадрата, то высоту пирамиды можно найти, используя свойства квадрата и теорему Пифагора.
Формула для нахождения высоты пирамиды с квадратным основанием
Для нахождения высоты пирамиды с квадратным основанием можно использовать следующую формулу:
H = √[(a√2/2cosα)^2 - (a√2/2)^2] = √[a^2/2*(1-cos^2α)/√cos^2α] = a*tgα/√2
где [(1-cos^2α)/cos^2α = tg^2α].
Нахождение высоты пирамиды с треугольным основанием
Если основание пирамиды является правильным треугольником, то высота будет образовывать с ребром пирамиды прямоугольный треугольник. Меньший катет проходит через высоту основания. В правильном треугольнике высота одновременно является и медианой. Из свойств правильного треугольника известно, что меньший его катет равен a√3/3. Зная угол между ребром пирамиды и плоскостью основания, можно найти гипотенузу (она же является ребром пирамиды). Высоту пирамиды можно определить по теореме Пифагора.
Формула для нахождения высоты пирамиды с треугольным основанием
Формула для нахождения высоты пирамиды с треугольным основанием выглядит следующим образом:
H = a*tgα/√3
Нахождение высоты пирамиды с пятиугольным или шестиугольным основанием
Если основание пирамиды является пятиугольником или шестиугольником, то она также считается правильной, если все стороны основания равны. Для нахождения высоты пирамиды с пятиугольным основанием, можно использовать следующую формулу:
h = √5+2√5a/2
Это свойство можно использовать для нахождения ребра пирамиды, а затем и ее высоты. Меньший катет равен половине этой высоты: k = √5+2√5a/4.
Формула для нахождения высоты пирамиды с пятиугольным или шестиугольным основанием
Используя формулу для нахождения меньшего катета и угла между ребром пирамиды и плоскостью основания, можно найти гипотенузу прямоугольного треугольника:
k/cosα = √5+2√5a/4cosα
Затем, как и в предыдущих случаях, высоту пирамиды можно найти по теореме Пифагора: