Как решать комплексные числа
- Математический анализ и его сложности
- Что такое комплексные числа?
- Представление комплексных чисел
- Операции над комплексными числами
- Вычисление модуля комплексного числа
- Решение примеров без специальных формул
Математический анализ и его сложности
Математический анализ является обязательным предметом для студентов технических вузов России. Однако, одной из самых трудных тем первого семестра для большинства студентов является решение комплексных чисел. В то же время, при более внимательном рассмотрении, становится понятно, что решение комплексных чисел может быть достигнуто с помощью простых алгоритмов.
Что такое комплексные числа?
Комплексные числа используются для расширения множества вещественных чисел. В отличие от вещественных чисел, которые можно представить на координатной прямой, для представления комплексного числа требуется две координатные оси (абсцисс и ординат). Комплексные числа могут получаться, например, при наличии у квадратного уравнения дискриминанта меньше нуля.
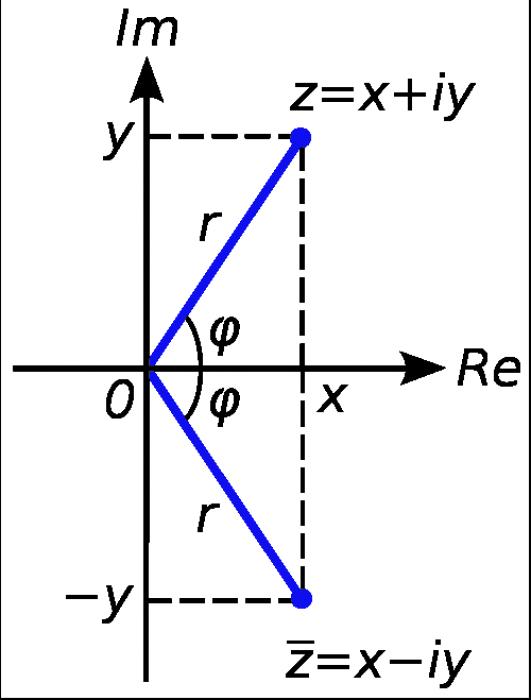
Представление комплексных чисел
Любое комплексное число может быть представлено в виде суммы x+yi, где число x - вещественная часть комплексного числа c, а число y - мнимая. Символ i в данном случае называется мнимой единицей, она равна квадратному корню из минус единицы.
Операции над комплексными числами
Для выполнения операций сложения и вычитания над парами комплексных чисел достаточно запомнить простое правило: вещественные части складываются или вычитаются отдельно, а мнимые части также складываются или вычитаются отдельно. То есть: (x1+y1*i)+(x2+y2*i)=(x1+x2)+(y1+y2)*i.
Умножение и деление комплексных чисел является более сложным процессом, однако в конечном итоге все сводится к тривиальным формулам. Эти формулы представлены на рисунке и получены с использованием обычных алгебраических преобразований, учитывая то, что комплексные числа складываются по частям, а квадрат мнимой единицы равен отрицательной единице.
Вычисление модуля комплексного числа
Иногда задания требуют вычислить модуль комплексного числа. Для этого необходимо извлечь квадратный корень из суммы вещественной и мнимой частей комплексного числа. Таким образом, получается численное значение модуля комплексного числа.
Решение примеров без специальных формул
В большинстве случаев решение примеров с комплексными числами можно выполнить без использования специальных формул. Достаточно использовать определение комплексного числа и алгебраические преобразования.






