Как решать матричное уравнение
- Решение матричного уравнения
- Перемножение матриц
- Обратная матрица
- Примеры
- Пример 1: Найдем обратную матрицу для А^-1.
- Заключение
Решение матричного уравнения
Решение матричного уравнения может показаться сложной задачей, однако оно не такое уж и сложное. Для того чтобы справиться с этой задачей, необходимо знать, как перемножать матрицы и находить их обратные. Давайте освежим нашу память и вспомним, как это делается.
Перемножение матриц
Перемножение матриц называется "строка на столбец". Матрицы А и В могут быть перемножены, если число столбцов в матрице А равно числу строк в матрице В. Эта операция обозначается символом "×" или просто АВ. Если С = АВ, то элементы матрицы С получаются перемножением элементов А и В по определенному правилу.
Обратная матрица
Для каждой невырожденной квадратной матрицы А (определитель |A| не равен нулю) существует единственная обратная матрица, обозначаемая А^-1. Эта матрица удовлетворяет условию А^-1 × А = А и называется единичной матрицей, где все элементы на главной диагонали равны единице, а остальные элементы равны нулю. Обратная матрица вычисляется по определенному правилу.
Примеры
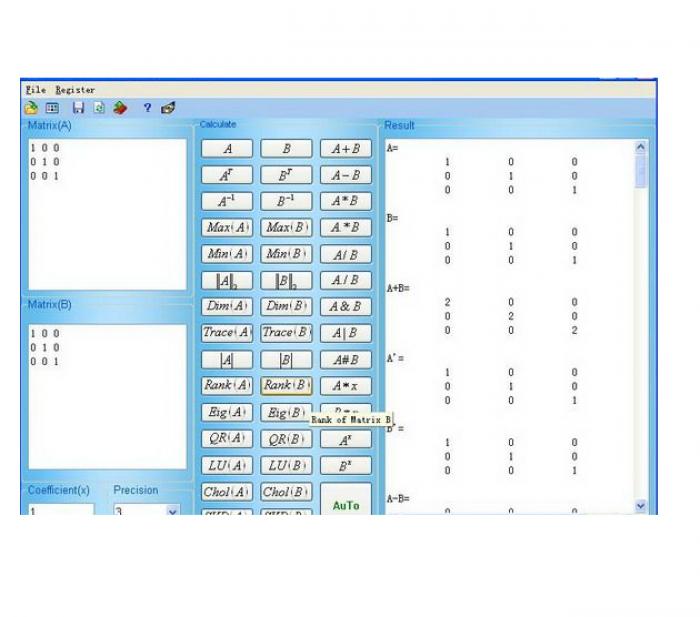
Пример 1: Найдем обратную матрицу для А^-1.
Пример 2: Решим матричное уравнение с использованием матрицы коэффициентов А из предыдущего примера и матрицы В.
Заключение
Матричные уравнения появились для решения систем линейных уравнений. Они представляют собой компактный алгоритм решения системы уравнений в матричной форме. Решение матричного уравнения состоит в умножении его на обратную матрицу слева. Матрицы Х и В могут иметь различную размерность.
Таким образом, решение матричного уравнения может быть достигнуто с помощью перемножения матриц и нахождения обратной матрицы.