Как соотносятся градусы и радианы

Содержание:

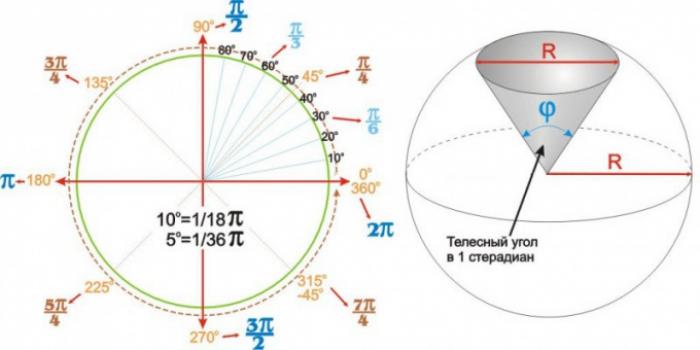
1. Углы в радианах и стерадианах: удобство и применение
2. Исторические корни системы измерения углов
3. Радианы: удобство и точность
4. Плоские углы в радианах
5. Сферические углы
6. Конкретизация углов

Углы в радианах и стерадианах: удобство и применение

Выражение углов в долях окружности является удобным и распространенным подходом в науке и технике. В этой системе угол, выраженный в радианах, представляет собой долю от полной окружности, которая равна двум пи радианам. Также важным понятием является телесный угол, который измеряется в стерадианах. Диаметр основания телесного угла соответствует диаметру сферы, из которой вырезан его сектор.

Исторические корни системы измерения углов

Интересно отметить, что разбиение окружности на 360 градусов было придумано древними вавилонянами. Основание системы счисления, равное числу 60, позволяет удобно представить десятичную, двенадцатиричную и троичную основы. Вавилонский алфавит содержал несколько сотен слоговых знаков, что позволяло выделить 60 под 60-ричные цифры.

Радианы: удобство и точность

С развитием математики и науки стало понятно, что выражение угла в радианах удобнее и точнее. Число пи, которое представляет отношение длины окружности к ее диаметру, является бесконечной непериодической десятичной дробью, которую невозможно записать в виде отношения целых чисел. Однако, в выражении тригонометрических функций, таких как синус, малых углов, использование радианов позволяет заменить сложные тригонометрические уравнения простыми арифметическими операциями.

Плоские углы в радианах

В науке и технике часто используется радиус окружности вместо диаметра для удобства расчетов. Поэтому было решено считать, что полная окружность равна 360 градусам или двум пи радианам. Таким образом, в одном радиане содержится примерно 57,3 угловых градуса. Для упрощения расчетов, можно использовать следующие соотношения: 5 градусам соответствует 1/36 пи радиана, а 10 градусам - 1/18 пи радиана. Таким образом, значения наиболее часто используемых углов, выраженных в радианах через пи, можно легко вычислить умножением числителя на пи.

Сферические углы

Однако в науке и технике также существуют сферические углы, которые измеряются в стерадианах. Телесный угол в 1 стерадиан является углом при вершине шарового сектора с диаметром основания, равным диаметру окружности. Важно отметить, что в научно-техническом лексиконе не существует "стеградусов".

Конкретизация углов

Для избежания путаницы, важно четко разделять плоские и сферические углы. При использовании технических значений углов, необходимо ясно указывать их конкретные характеристики. Например, "угловое расстояние на небесной сфере между звездами А и Б составляет 13 градусов 47 минут дуги" или "объект наблюдался под курсовым углом в 123 градуса и был виден под телесным углом примерно в 2 градуса".