Как составить уравнение параболы
- Уравнение параболы: основы и варианты
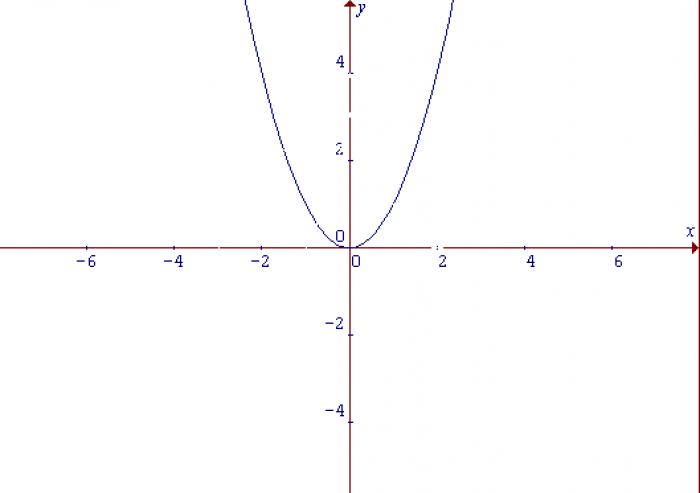
- Простейшая функция: y=x^2
- Варианты построения параболы и ее уравнение
- Параболические зависимости
- Примеры параболы в физических задачах
Уравнение параболы: основы и варианты
Уравнение параболы является квадратичной функцией и имеет несколько вариантов составления в зависимости от представленных параметров. Парабола представляет собой кривую, напоминающую дугу и являющуюся графиком степенной функции. Независимо от характеристик параболы, функция всегда является четной.
Простейшая функция: y=x^2
Начнем с самой простой функции параболы: y=x^2. Эта функция возрастает как при положительных, так и при отрицательных значениях аргумента x. Точка (0,0) считается точкой минимума функции.
Варианты построения параболы и ее уравнение
Существует несколько вариантов построения и уравнения параболы. Рассмотрим первый пример: функция вида f(x)=x^2+a, где a - целое число. Чтобы построить график данной функции, необходимо сдвинуть график функции f(x) на a единиц. Например, функция y=x^2+3 сдвигает график вверх на 3 единицы. Если дана функция с противоположным знаком, например y=x^2-3, то ее график сдвигается вниз по оси y.
Еще один вид функции, задающей параболу, это f(x)=(x +a)^2. В этом случае график сдвигается вдоль оси x на a единиц. Например, функции y=(x +4)^2 и y=(x-4)^2 сдвигают график по оси x влево и вправо соответственно.
Параболические зависимости
Существуют также параболические зависимости вида y=x^4. При таких случаях x является константой, а y резко возрастает. Однако это относится только к четным функциям.
Примеры параболы в физических задачах
Графики параболы часто встречаются в физических задачах. Например, полет тела описывает линию, напоминающую параболу. Также вид параболы имеет продольное сечение рефлектора фары или фонаря. В отличие от синусоиды, параболический график является непериодическим и возрастающим.
