Как вычислить длину вектора
- Векторы и их роль в математике и физике
- Определение вектора в различных системах координат
- Модуль вектора и его вычисление
- Вычисление длины вектора в декартовых координатах на плоскости
- Универсальная формула для вычисления длины вектора в пространстве
Векторы и их роль в математике и физике
Векторы — отрезки, которые имеют не только длину, но и направление. Они играют важную роль в математике, особенно в физике, где часто используются для представления различных величин. В математических и физических расчетах может возникнуть необходимость вычислить длину вектора, заданного координатами.
Определение вектора в различных системах координат
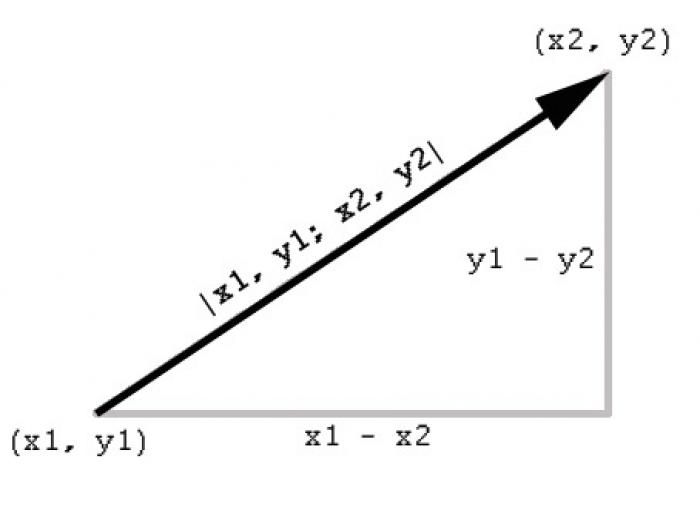
В любой системе координат вектор определяется через две точки, начало и конец. В декартовых координатах на плоскости вектор обозначается как (x1, y1; x2, y2), а в трехмерном пространстве - (x1, y1, z1; x2, y2, z2). Векторы также могут быть определены для пространств большей размерности. Хотя их представление может быть сложным, математические вычисления остаются теми же.
Модуль вектора и его вычисление
Модуль вектора также называется его длиной. Если A - вектор, то |A| - число, равное его модулю. Модуль вектора не зависит от его направления. Например, модуль вектора (0; -2) равен 2.
Вычисление длины вектора в декартовых координатах на плоскости
В декартовых координатах на плоскости, вычисление длины вектора проще всего, если его начало совпадает с началом координат. Длина вектора вычисляется как квадратный корень из суммы квадратов координат его конца. Например, для вектора A = (0, 0; 3, 4), его модуль |A| = √(3^2 + 4^2) = 5. Вычисление модуля вектора сводится к применению формулы Пифагора для прямоугольного треугольника, где координатные отрезки, задающие вектор, являются катетами, а вектор - гипотенузой.
Вычисление длины вектора, когда начало не совпадает с началом координат
Когда начало вектора не находится в точке отсчета координат, вычисление его длины становится сложнее. В этом случае, вместо координат конца вектора, возводят в квадрат разности между координатой конца и соответствующей координатой начала. Если координата начала равна нулю, формула превращается в предыдущую. Вычисление длины вектора по-прежнему использует теорему Пифагора. Если A = (x1, y1; x2, y2), то |A| = √((x2 - x1)^2 + (y2 - y1)^2). Например, для вектора A = (1, 2; 4, 6), его модуль равен |A| = √((4 - 1)^2 + (6 - 2)^2) = 5.
Универсальная формула для вычисления длины вектора в пространстве
Формула для вычисления длины вектора в пространстве также является универсальной и может быть обобщена для векторов с большим количеством координат. Длина вектора всегда равна квадратному корню из суммы квадратов разностей координат конца и начала.
Векторы являются важным инструментом в математике и физике. Вычисление их длины, или модуля, может быть выполнено в различных системах координат с использованием формулы Пифагора. Знание и понимание этих концепций помогает в решении различных задач и применении векторов в практических ситуациях.