Как вычислить основание равнобедренного треугольника

Содержание:

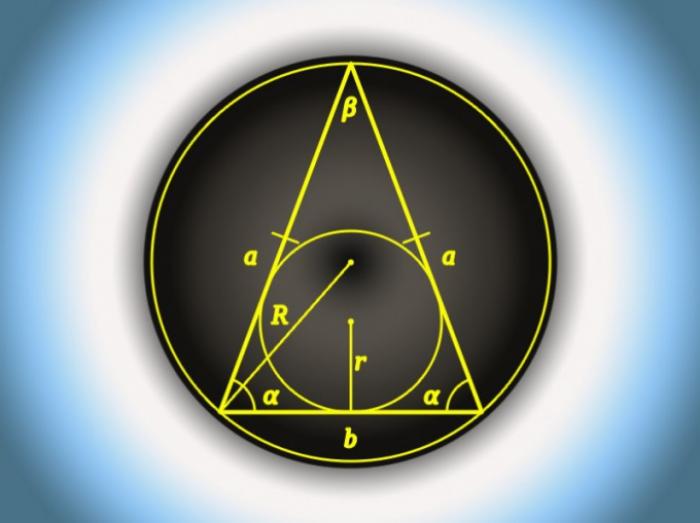
1. Вычисление длины основания равнобедренного треугольника
2. Использование теоремы о проекциях
3. b = 2*a*cos(α)
4. Использование синуса и половины величины угла
5. b = 2*a*sin(β/2)
6. Вычисление основания с использованием корня
7. b = a*√(2*(1-cos(β)))
8. Простой расчет по периметру и боковой стороне
9. b = P-2*a
10. Вычисление основания по площади и высоте
11. b = 2*S/h
12. Использование высоты и боковой стороны
13. b = 2*√(h²-a²)
14. b = 2*R*sin(β)

Вычисление длины основания равнобедренного треугольника

В равнобедренном треугольнике основание - это сторона, которая отличается по длине от двух других. Если все три стороны равны, то любую из них можно считать основанием. Вычисление длины основания может быть выполнено различными способами в зависимости от известных параметров треугольника.

Использование теоремы о проекциях

Для вычисления длины основания (b) равнобедренного треугольника, когда известна длина боковой стороны (a) и величина угла при основании (α), можно использовать теорему о проекциях. Согласно этой теореме, длина основания равна двум длинам боковой стороны, умноженным на косинус угла α:

b = 2*a*cos(α)

Использование синуса и половины величины угла

Если известна длина боковой стороны (a) и угол, лежащий напротив основания (β), можно использовать синус и половину величины угла для вычисления длины основания (b). Длину основания можно получить, умножив два значения (sin(β/2) и a) и удвоив результат:

b = 2*a*sin(β/2)

Вычисление основания с использованием корня

Для треугольников с заданными значениями боковой стороны (a) и угла при вершине (β) существует еще одна формула, где помимо тригонометрической функции используется извлечение корня. Для вычисления длины основания (b) отнимите от единицы косинус угла при вершине, удвойте полученное значение, извлеките из результата корень и умножьте на длину боковой стороны:

b = a*√(2*(1-cos(β)))

Простой расчет по периметру и боковой стороне

Если известна длина периметра (P) и боковой стороны (a) равнобедренного треугольника, то длину основания (b) можно легко вычислить путем вычитания двух вторых значений из первого:

b = P-2*a

Вычисление основания по площади и высоте

Для равнобедренных треугольников с известными значениями площади (S) и высоты (h) можно рассчитать длину основания (b). Для этого необходимо удвоенную площадь разделить на высоту:

b = 2*S/h

Использование высоты и боковой стороны

Высота (h), опущенная на основание (b), может быть использована для вычисления длины основания (b) в сочетании с длиной боковой стороны (a). Если значения этих двух параметров известны, то вычисление длины основания можно выполнить следующим образом: возвести высоту в квадрат, вычесть из полученного значения квадрат длины боковой стороны, извлечь квадратный корень и удвоить результат:

b = 2*√(h²-a²)

Вычисление основания через радиус описанной около треугольника окружности

Если известен угол, лежащий напротив основания (β), и радиус (R) окружности, описанной вокруг равнобедренного треугольника, можно использовать следующую формулу для вычисления длины основания (b):

b = 2*R*sin(β)