Как вычислить площади граней пирамиды
- Пирамида и ее свойства
- Вычисление площади боковых граней
- Вычисление площади грани с известными длинами всех трех боковых ребер
- Вычисление площади грани с известной высотой и длиной общего ребра
- Вычисление площади грани с известным периметром основания и апофемой
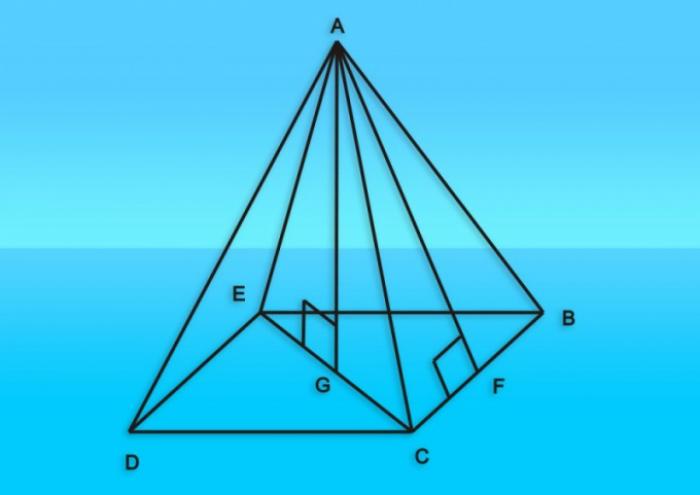
Пирамида и ее свойства
Пирамида - это геометрическая фигура, которая является частным случаем конуса. У пирамиды в основании лежит многоугольник, что определяет наличие плоских боковых граней. В произвольной пирамиде размеры боковых граней могут быть разными, что усложняет вычисление их площади.
Вычисление площади боковых граней
Если речь идет о пирамиде правильной формы, то вычисление площади боковых граней значительно упрощается. В зависимости от известных параметров, можно использовать различные формулы для вычисления площади каждой боковой грани.
Вычисление площади грани с известной апофемой и длиной одного из боковых ребер
Если известны апофема (h) и длина одного из боковых ребер (b) грани, то площадь (s) можно найти по формуле: s = h*b/2.
Вычисление площади грани с известными длинами обоих боковых ребер и углом между ними
Если известны длины обоих боковых ребер (b и c) и угол (γ) между ними, то площадь (s) можно найти по формуле: s = ½*b*c*sin(γ).
Вычисление площади грани с известными длинами всех трех боковых ребер
Если известны длины всех трех боковых ребер (a, b, c), то площадь (s) можно найти с помощью формулы Герона: s = √(p*(p-a)*(p-b)*(p-c)), где p = (a+b+c)/2 - полупериметр грани.
Вычисление площади грани с известной высотой и длиной общего ребра
В прямоугольной пирамиде площадь (s) грани, прилегающей к прямому углу, можно найти по высоте (H) и длине общего ребра (a) с основанием. Формула вычисления: s = H*a/2.
Вычисление площади грани с известным периметром основания и апофемой
В пирамиде правильной формы, если известны периметр основания (P) и апофема (h), площадь (s) грани можно найти по формуле: s = ½*P*h.
Вычисление площади грани с известным числом вершин многоугольника основания и углом между боковыми ребрами
При известном числе вершин (n) в многоугольнике основания и угле (α) между боковыми ребрами, площадь (s) грани можно найти по формуле: s = ½*n*b²*sin(α), где b - длина бокового ребра.
Зная эти формулы, можно легко вычислить площади боковых граней пирамиды различных форм и размеров.