Как вычислить производную функции
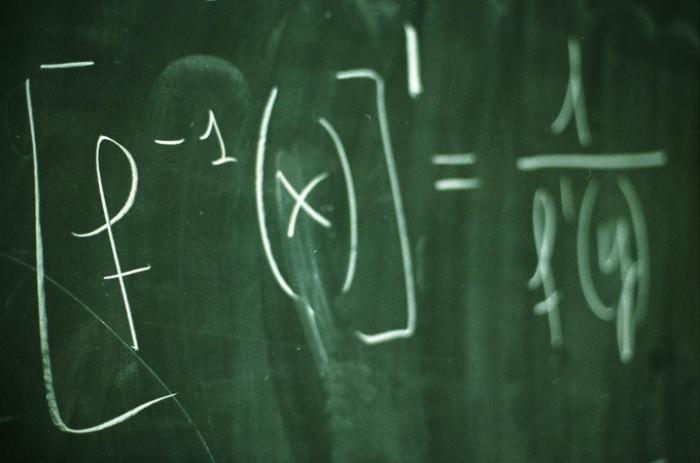
- Понятие производной и его применение в науке
- Основные правила дифференцирования
- Таблица производных
- Правила дифференцирования простых функций
- Правила дифференцирования для суммы и разности функций
- Правило дифференцирования для произведения функций
- Правило дифференцирования для частного функций
- Правило дифференцирования для сложной функции
- Вычисление производной высшего порядка
- Заключение
Понятие производной и его применение в науке
Понятие производной широко используется во многих областях науки и является одной из базовых задач математики. Производная позволяет найти скорость изменения функции в каждой ее точке и играет важную роль в физике, экономике, биологии и других научных дисциплинах.
Основные правила дифференцирования
Для нахождения производной любой функции необходимо знать несложные правила дифференцирования. Ниже представлены основные правила, которые помогут вам вычислить производную любой функции.
Таблица производных
Для быстрого вычисления производных первым делом стоит запомнить таблицу производных основных элементарных функций. Такая таблица позволит вам найти производную простой функции от одной переменной. Например, производная от квадратного корня из x равна 1/(2×√(x)).
Правила дифференцирования простых функций
Помимо таблицы производных, необходимо изучить основные правила дифференцирования. Если дана функция от одной переменной, вы можете использовать правила для вычисления производной. Например, производная от 2×sin(x) равна 2×cos(x).
Правила дифференцирования для суммы и разности функций
Если вам нужно найти производную суммы или разности двух функций, вычислите производные каждого слагаемого и затем сложите их. Например, производная от x²+x³ равна 2×x+3×x².
Правило дифференцирования для произведения функций
Для вычисления производной произведения двух функций используйте формулу, которая представляет собой сумму произведений производной первой функции на вторую функцию и производной второй функции на первую функцию. Например, производная от √(x)×tg(x) равна tg(x)/(2×√(x))+√(x)/cos²(x).
Правило дифференцирования для частного функций
Если ваша функция представляет собой частное двух функций, используйте формулу для вычисления производной, которая представляет собой разность произведения производной первой функции на вторую функцию и произведения первой функции на производную второй функции, деленную на квадрат второй функции. Например, производная от sin(x)/x равна (cos(x)×x-sin(x))/x².
Правило дифференцирования для сложной функции
Если вам нужно вычислить производную сложной функции, то есть функции вида f(g(x)), используйте правило, которое представляет собой произведение производной внешней функции на производную внутренней функции. Например, производная от sin(x)³ равна 3×(sin(x))²×cos(x).
Вычисление производной высшего порядка
Если ваша задача состоит в вычислении производной высшего порядка, то вычислите последовательно производные низшего порядка. Например, производная второго порядка от x³ равна 6×x.
Заключение
Знание правил дифференцирования позволяет быстро и точно вычислять производные функций в различных областях науки. Основные правила и таблица производных помогут вам в этом процессе. При использовании данных правил, не забывайте обозначать взятие производной символом ' и возведение в степень символом ^.