Как вычислять координаты точек пересечения парабол

Содержание:

1. Как найти точки пересечения парабол на плоскости
2. Шаг 1: Получение уравнений парабол
3. Шаг 2: Вычитание уравнений парабол
4. Шаг 3: Нахождение корней квадратного уравнения
5. Шаг 4: Подстановка значений корней в уравнение параболы
6. Особый случай

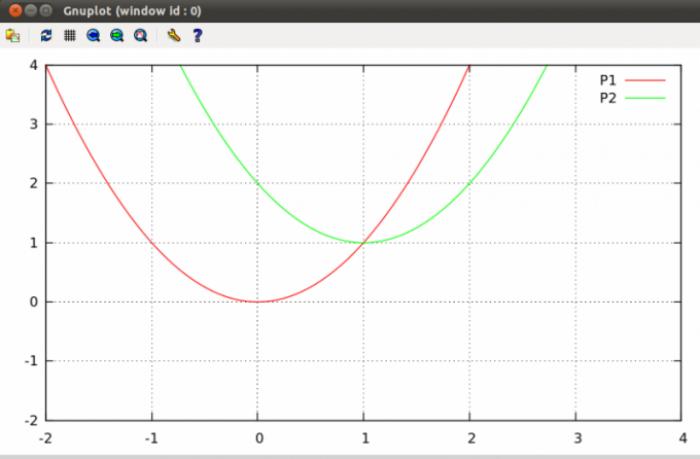
Как найти точки пересечения парабол на плоскости

Параболы на плоскости могут иметь различное количество точек пересечения. Некоторые параболы могут пересекаться в одной точке, другие - в двух точках, а некоторые вообще могут не иметь точек пересечения. Поиск таких точек является типичной задачей алгебры и входит в программу школьного курса. Для нахождения точек пересечения парабол необходимо выполнить несколько шагов.

Шаг 1: Получение уравнений парабол

Первым шагом в решении данной задачи является получение уравнений обеих парабол. Парабола на плоскости может быть задана уравнением вида y = ax² + bx + c (формула 1), где a, b и c - произвольные коэффициенты, при условии, что a ≠ 0. Для данной задачи пусть у нас имеются две параболы с уравнениями y = 2x² - x - 3 и y = x² - x + 1.

Шаг 2: Вычитание уравнений парабол

Вторым шагом необходимо вычесть одно уравнение параболы из другого. Вычитание уравнений позволяет получить полином второй степени, коэффициенты которого можно легко вычислить. Для нахождения точек пересечения парабол, необходимо поставить знак равенства нулю и решить полученное квадратное уравнение. В нашем случае получим уравнение y = x² - 4 = 0.

Шаг 3: Нахождение корней квадратного уравнения

Третий шаг состоит в нахождении корней квадратного уравнения. Для этого используется соответствующая формула, которая приведена в учебниках алгебры. В данном примере уравнение y = x² - 4 = 0 имеет два корня: x = 2 и x = -2. Обратите внимание, что в общем случае квадратное уравнение может иметь два корня, один корень или не иметь корней. В последнем случае параболы не пересекаются и задача не имеет решения.

Шаг 4: Подстановка значений корней в уравнение параболы

Четвертый шаг заключается в подстановке найденных корней в уравнение параболы. В нашем примере, подставив x = 2, получим y = 3, а при x = -2, получим y = 7. Таким образом, точки пересечения парабол на плоскости равны (2;3) и (-2;7). Обратите внимание, что у данных парабол нет других точек пересечения.

Особый случай

Особым случаем является поиск точек пересечения тождественно равных парабол, то есть двух парабол, задаваемых одинаковыми уравнениями. В этом случае все точки пересечения совпадают, так как параболы идентичны.