Как вычислять определитель матрицы
- Определитель матрицы: основные понятия
- Вычисление определителя по первой формуле
- Вычисление определителя по второй формуле
- Определитель единичной матрицы
Определитель матрицы: основные понятия
Определитель или детерминант матрицы - это некоторое число, вычисляемое по особым формулам, составленным из комбинаций ее членов. Определитель можно вычислить только для квадратной матрицы.
Вычисление определителя по первой формуле
Чтобы рассчитать определитель матрицы по первой формуле, необходимо выполнить следующие шаги:
- Суммируем произведения коэффициентов, стоящих в первой строке, с определителем матрицы, полученной из исходной вычеркиванием столбца и строки, в которых стоит умножаемый коэффициент.
- Знаки у сомножителей будут чередоваться: у первого будет "+", у второго будет "-" и так далее.
Эта формула верна для элементов любых строк - необязательно брать первую, но это удобнее для наглядности.
Вычисление определителя по второй формуле
Существует также алгоритм вычисления определителя матрицы по второй формуле:
- Вводим понятие главной диагонали матрицы - это элементы, стоящие по диагонали, начиная с а11 и заканчивая а(nn).
- Для матрицы из одного элемента определитель будет равен значению этого элемента.
- Для матрицы 2x2 определитель будет разностью произведений элементов, стоящих на главной и побочной диагонали.
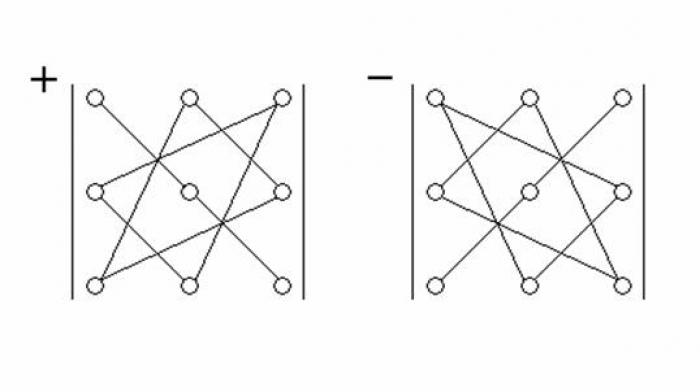
- Для матрицы 3x3 сначала подписываем первые два столбца справа от третьего. Получается матрица 3x5, где суммируются произведения элементов по трем главным и побочным диагоналям. Эти суммы вычитаются и полученное число становится определителем матрицы.
- Для матрицы 4x4, 5x5 и т.д. применяется аналогичное правило, но возникают сложности в связи с большим количеством чисел и операций, поэтому часто используется первый способ вычисления.
Определитель единичной матрицы
Отметим, что определитель единичной матрицы всегда равен единице. Это легко проверить.