Как взять производную
- Производные в математике: необходимость и простой алгоритм
- Основной алгоритм взятия производных
- Сложные функции и взятие их производных
Производные в математике: необходимость и простой алгоритм
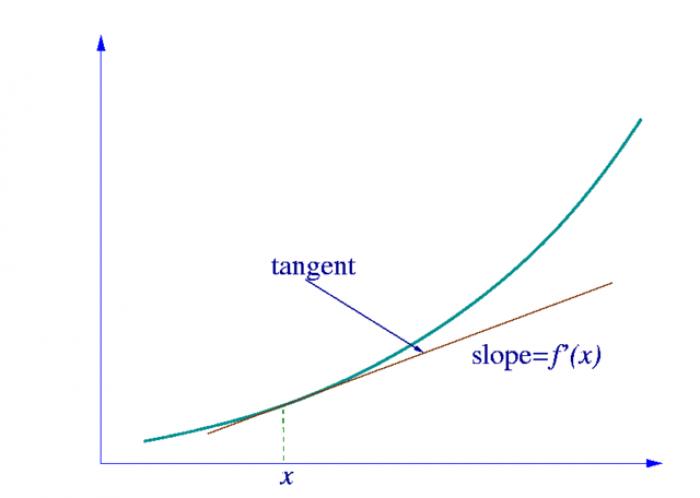
Умение брать производную является неотъемлемой частью математического образования, начиная с 9 класса средней школы. Большое количество заданий на производные встречается и на экзамене ЕГЭ по математике. Более того, студенты высших учебных заведений также должны уметь брать производные любых функций. Но несмотря на сложность восприятия этой темы, существует простой алгоритм для взятия производных.
Основной алгоритм взятия производных
Для начала необходимо определить вид функции, производную которой мы ищем. Если это простая функция от одной переменной, мы можем использовать таблицу основных производных для ее вычисления.
Производная суммы функций равна сумме производных этих функций. То есть, если у нас есть функции f(x) и g(x), производная их суммы будет равна сумме производных этих функций.
Производная произведения функций f(x) и g(x) вычисляется как сумма произведений производной первой функции на вторую функцию и производной второй функции на первую функцию.
Производную частного можно найти по формуле (f(x)'*g(x)-g(x)'*f(x))/(g(x)^2). Эта формула практически идентична производной от произведения, за исключением знака - в числителе производной от произведения вычитается, а знаменатель представляет собой квадрат знаменателя исходной функции.
Сложные функции и взятие их производных
Самой сложной операцией при взятии производной является взятие производной сложной функции, то есть функции вида f(g(x)). В этом случае необходимо сначала найти производную внешней функции, не обращая внимания на вложенную функцию. Затем, вычислив производную внутренней функции, мы домножаем ее на производную от внешней функции, рассматривая внутреннюю функцию как аргумент.
Полезным советом является умение отличать внешнюю функцию от внутренней. Можно слегка обвести внутреннюю функцию и рассматривать ее как простую переменную временно, чтобы избежать путаницы при вычислении производной сложной функции.
Таким образом, умение брать производные является необходимым навыком для учеников средней школы и студентов высших учебных заведений. Простой алгоритм взятия производных существует и помогает в решении задач и экзаменов. Важно понимать основные правила взятия производных и уметь применять их на практике.






