Как найти сторону правильного многоугольника
- Понятие многоугольников
- Правильные многоугольники
- Нахождение сторон равностороннего треугольника
- Нахождение стороны квадрата
- Связь стороны и радиуса вписанной или описанной окружности
- Общая формула для нахождения стороны многоугольника
Понятие многоугольников
Фигура, образованная более чем из двух линий, замыкающихся между собой, называется многоугольником. Каждый многоугольник имеет вершины и стороны. Любой из них может быть правильным или неправильным.
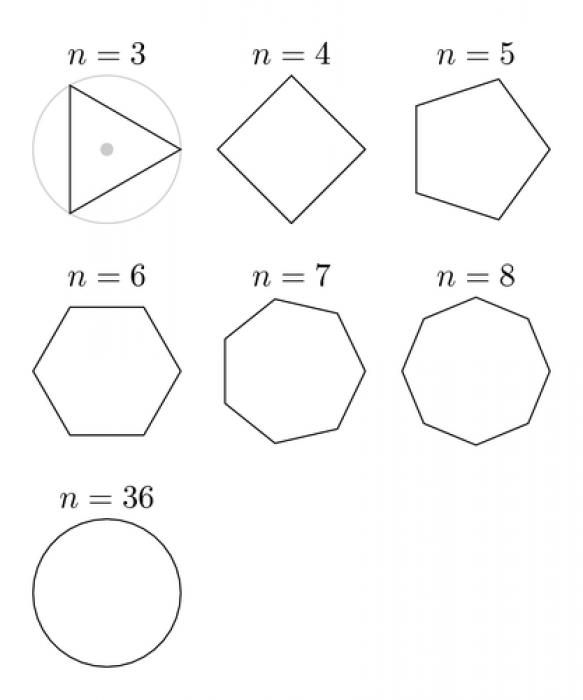
Правильные многоугольники
Правильным многоугольником называется фигура, у которой все стороны равны. Например, равносторонний треугольник представляет собой правильный многоугольник, состоящий из трех замкнутых линий. В данном случае, все его углы равны 60°. Его стороны между собой равны, но не параллельны друг другу. Таким же свойством обладают и другие многоугольники, однако, углы у них имеют другие величины. Единственный из правильных многоугольников, у которого стороны не только равны, но и попарно параллельны - квадрат.
Нахождение сторон равностороннего треугольника
Если в задаче дан равносторонний треугольник с площадью S, то его неизвестную сторону можно найти через углы и стороны. Преобразуя формулу для нахождения площади, можно вычислить длину стороны треугольника.
Нахождение стороны квадрата
Строны правильного четырехугольника, который является квадратом, можно найти, используя его площадь или диагональ.
Связь стороны и радиуса вписанной или описанной окружности
В большинстве случаев сторону правильного многоугольника можно определить, зная радиус вписанной в него или описанной вокруг него окружности. Формулы связывают сторону и радиус окружности в зависимости от типа многоугольника.
Общая формула для нахождения стороны многоугольника
Для всякого произвольного n-угольника формула для нахождения стороны в общем виде выглядит следующим образом: a=2Rsin(α/2)=2rtg(α/2)