Чем поможет знание геометрии в будущем

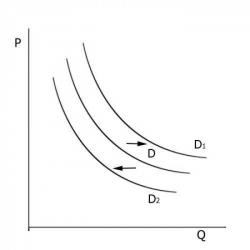
Полезность геометрии в повседневной жизни
Недостаток жизненного опыта позволяет некоторым школьникам и даже студентам думать, что больше половины изучаемых предметов абсолютно бесполезны и никогда не пригодятся в жизни. На самом деле, знания могут придти на помощь в неожиданный момент, и доставать учебники уже не будет времени. Одна из полезнейших наук — геометрия, некоторые виды деятельности без нее немыслимы.
Геометрия в строительстве и ремонте
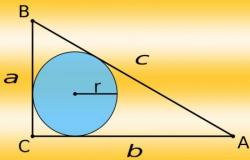
Без знания геометрии невозможно построить дом или отремонтировать квартиру. Например, при установке стропил на крышу понадобится формула расчета высоты треугольника, особенно, если крыша несимметричная. Без этого нельзя будет рассчитать длину перекладин, а также узнать количество кровельного материала. Чтобы посчитать количество блоков или кирпичей для стены, плиток для ремонта ванной комнаты, досок для пола — необходимы знания формул площади поверхности, а для объемных покрытий, например, утеплителей — формул объема. Для разработки системы вентиляции, обогрева, канализации или водоснабжения в доме или квартире потребуется расчет внутреннего объема труб, а это невозможно сделать без формулы площади круга. Конечно, можно доверить это профессионалам — но без знания геометрии будет невозможно даже разобраться в чертежах и проверить качество работы. Вообще, чертежи встречаются даже далекому от них человеку на протяжении всей жизни. Это чертеж дома или план ремонта, чертежи деталей на заводе, знать которые нужно не только конструктору и технологу, но и токарю, сварщику, контролеру, менеджерам отделов закупок и продаж. С чертежами непременно столкнется автолюбитель, который захочет провести ремонт своей машины.
Значение тригонометрии
Незаменима тригонометрия при работе с земельным участком, например, при строительстве дома или разметке грядок. Разметить ровные параллельные линии, создать аккуратный симметричный дизайн цветника можно только с помощью геометрических формул. При измерении дальних расстояний не обязательно тянуть рулетку — можно просто измерить угол от ближайшего столба или стены и, зная формулу тангенсов или синусов, вычислить расстояние. Обычно этим занимаются геодезисты. Косинусы и синусы нужны также электротехникам, например, с их помощью можно рассчитать, на сколько изменится сила тока через определенное время. Без них невозможно начертить разделить круг на равные сектора — это умение может пригодится в самых разных областях жизни, от рисования и дизайна до раскраивания ткани или строительных материалов. Вообще, тригонометрические функции нужны в основном инженерам и ученым. Именно с их помощью были созданы все современные достижения техники — планшеты и смартфоны, компьютеры и «умная» бытовая техника. В обычной же жизни они требуются редко, в основном для того, чтобы помочь подросшим детям готовить домашние задания. Тем не менее, изучение тригонометрии необычайно полезно для мозга — поиск нужных формул, трансформация одних элементов в другие заставляет извилины напрягаться, и мозг будет более подвижным всю жизнь. После тригонометрических задач попытка в магазине другой страны перевести рубли в доллары и затем в местную валюту, вычесть процентную скидку (и все это без калькулятора, поскольку зарядка телефона села) и одновременно сравнить с ценами в трех предыдущих магазинах окажется детской игрой.