Как вписать круг в прямоугольный треугольник
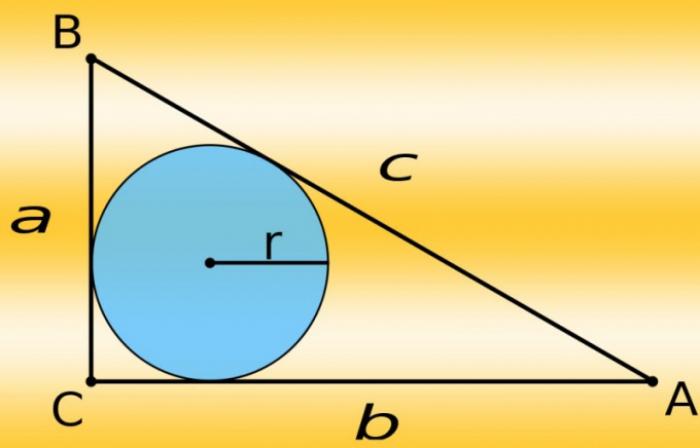
- Как построить вписанную окружность в прямоугольный треугольник?
- Шаг 1: Определение центра вписанной окружности
- Шаг 2: Определение радиуса вписанной окружности
- Шаг 3: Альтернативный способ построения
- Шаг 4: Построение точек касания
- Шаг 5: Проведение полукругов
Как построить вписанную окружность в прямоугольный треугольник?
Прямоугольный треугольник - это треугольник, один из углов которого равен 90°. В такой фигуре можно вписать круг, и в данной статье мы рассмотрим несколько способов построения вписанной окружности без использования формул и вычислений.
Шаг 1: Определение центра вписанной окружности
Найдите точку, которая станет центром вписанной окружности. Она должна лежать на пересечении биссектрис углов в вершинах треугольника. Для этого приложите транспортир к одному из углов и определите его величину. Затем отметьте вспомогательную точку на отметке, равной половине этой величины. Проведите отрезок из вершины этого угла, через вспомогательную точку и закончите его на противолежащей стороне. Точно также постройте биссектрису другого угла. Точка пересечения двух вспомогательных отрезков будет центром вписанной окружности.
Шаг 2: Определение радиуса вписанной окружности
Определите радиус вписанной окружности. Для этого проведите еще один вспомогательный отрезок, начинающийся в найденной точке и заканчивающийся на одном из катетов, параллельном другому катету. Длина этого отрезка будет радиусом вписанной окружности. Отложите его на циркуле и начертите круг с центром в найденной точке. Тем самым, построение вписанной окружности будет завершено.
Шаг 3: Альтернативный способ построения
Существует также альтернативный способ построения вписанной окружности с использованием формулы из курса элементарной геометрии. Для этого необходимо знать длины всех сторон треугольника. Измерьте их и затем рассчитайте радиус (r). Сложите длины катетов (a и b), отнимите от результата длину гипотенузы (c), и разделите полученное значение пополам: r = (a+b-c)/2. Отложите найденную величину на циркуле и не меняйте это расстояние до конца построения.
Шаг 4: Построение точек касания
Установите циркуль в вершину прямого угла и начертите вспомогательную дугу, которая должна пересечь оба катета. Вместо дуги можно также поставить метки на катетах, указывающие точки касания вписанной окружности и сторон треугольника.
Шаг 5: Проведение полукругов
Установите циркуль в каждую из точек касания и проведите два полукруга, лежащих внутри треугольника. Точка их пересечения - центр вписанной окружности. Установите циркуль в эту точку и проведите окружность, вписанную в прямоугольный треугольник.
Теперь вы знаете несколько способов построения вписанной окружности в прямоугольный треугольник. Пользуйтесь этими методами и достигайте точных результатов в геометрических построениях.