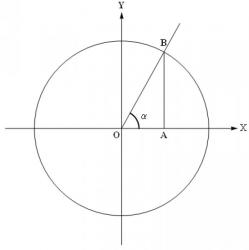
Что такое синус и косинус

- Изучение треугольников и теоремы синусов и косинусов
- Производные и их применение
- Применение синусов и косинусов
- Таблица косинусов для углов
Изучение треугольников и теоремы синусов и косинусов
Изучение треугольников и их свойств является одной из основных задач математики на протяжении многих веков. Для рассмотрения треугольников и вычисления их сторон и углов были введены специальные величины - синус и косинус. Их истоки связаны с прямоугольными треугольниками, где отношение сторон остается неизменным при неизменной градусной мере углов. Синус острого угла в прямоугольном треугольнике определяется как отношение противолежащего катета к гипотенузе, а косинус - как отношение прилежащего катета к гипотенузе.
Производные и их применение
Производная - это инструмент, который показывает, как быстро функция изменяется относительно своего аргумента. Производные широко применяются не только в математике, но и в других научных и технических дисциплинах. При решении различных задач, особенно связанных с треугольниками, необходимо знать производные тригонометрических функций, таких как синус и косинус. Производная синуса является косинусом, а производная косинуса - синусом с обратным знаком.
Применение синусов и косинусов
Синусы и косинусы имеют широкое применение в решении задач, связанных с треугольниками. Они позволяют удобно вычислять углы и стороны треугольников, используя теоремы косинусов и синусов. Особенно это полезно для инженеров и архитекторов, которые часто сталкиваются с расчетами соотношений сторон и углов.
Таблица косинусов для углов
Для удобства использования синусов и косинусов были созданы таблицы со значениями этих функций для различных углов. Одной из таких таблиц является таблица косинусов для углов от 0 до 360 градусов. Эта таблица позволяет легко находить значения косинуса для заданного угла.
Выводы:
Изучение треугольников и их свойств является фундаментальной задачей математики. Введение синуса и косинуса позволяет удобно рассчитывать стороны и углы треугольников, как в прямоугольных, так и в общих случаях. Производные синуса и косинуса имеют широкое применение в различных научных и технических областях. Таблицы значений синусов и косинусов упрощают вычисления и позволяют быстро получать нужные значения для заданного угла. Все это делает синусы и косинусы неотъемлемой частью математики и ее применения в реальных задачах.