Как брать интеграл
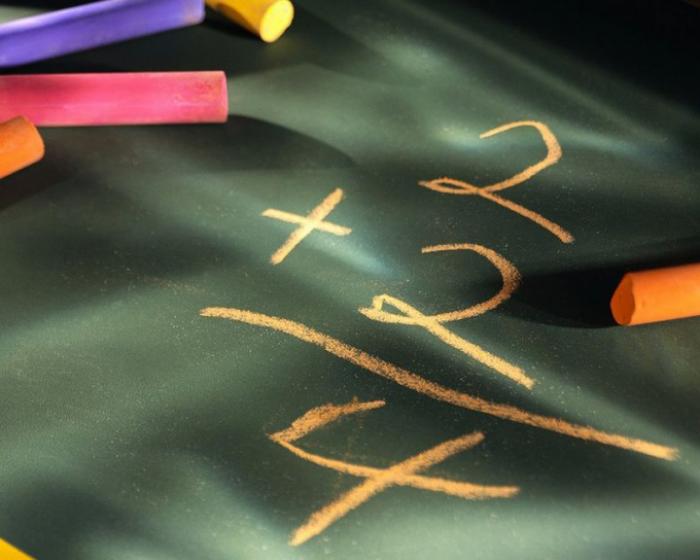
Введение
В математике существует несколько способов для "взятия" интеграла. Один из них - это нахождение первообразной функции. Первообразная функция F(x) определяется как функция, производная которой равна исходной функции f(x). Это понятие тесно связано с взятием интеграла.
Определение первообразной
Функция F(x) является первообразной функции f(x), если ее производная F’(x) равна f(x). Так как производная любой константы равна нулю, то первообразных функции f(x) существует бесконечно много. Все они отличаются друг от друга только на константу.
Определение неопределенного интеграла
Неопределенный интеграл обозначается символом ∫ и представляет собой процесс нахождения первообразной функции. Обозначение неопределенного интеграла представлено на рисунке 1.
Простейшие приемы интегрирования
Существует несколько простейших приемов интегрирования, которые основаны на свойствах неопределенных интегралов и тождественных преобразованиях подынтегральной функции. В данной статье рассмотрим два основных приема интегрирования.
Прием 1: Непосредственное интегрирование
Непосредственное интегрирование заключается в вычислении интегралов с помощью их определенных свойств и специальных таблиц. Например, интеграл ∫(4/(cosx^2)- 3cosx +2/(x-1))dx может быть вычислен следующим образом: ∫(4/(cosx^2)- 3cosx +2/(x-1))dx= 4∫dx/(cosx^2)- 3∫cosxdx +2∫dx/(x-1)=4tgx-3sinx+2ln|x-1| + C.
Прием 2: Разложение подынтегральной функции
Данный прием заключается в преобразовании подынтегральной функции, используя формулы алгебры и тригонометрии. Подынтегральная функция представляется в виде суммы функций, интегралы от которых можно легко брать. Например, ∫(1+(cosx)^2/(1+cos(2x))dx=[1+cos(2x)=2(cosx)^2 ]=∫(1+(cosx)^2/2(cosx)^2)dx==(1/2)∫1/(cosx)^2)dx+(1/2)∫dx=(1/2)(tgx+x)+C.
Прием 3: Подведение под знак дифференциала
Этот прием основан на свойстве инвариантности формул интегрирования. Подынтегральная функция преобразуется к виду f(u(x))u’(x), а затем сомножитель u’(x) подводится под знак дифференциала (интегрируется) – u’(x)dx=d(u(x)), после чего применяется формула ∫(f(u(x))du(x))=u(x)+C.
Заключение
В данной статье были рассмотрены основные приемы интегрирования. Непосредственное интегрирование, разложение подынтегральной функции и подведение под знак дифференциала - это лишь некоторые из способов для "взятия" интеграла. Используя эти приемы, можно значительно упростить процесс интегрирования и находить аналитические выражения для интегралов.