Как доказать, что точка не лежит в плоскости треугольника

- Как доказать, что точка не лежит в плоскости треугольника
- Шаг 1: Определение принадлежности сторон треугольника
- Шаг 2: Задание сторон треугольника
- Шаг 3: Проверка принадлежности точки
Как доказать, что точка не лежит в плоскости треугольника
Для того чтобы убедиться, что точка не находится в плоскости треугольника, можно выполнить простую проверку, рассмотрев все возможные ситуации. Однако необходимо помнить, что также существует противоположный случай, когда точка находится внутри треугольника.
Шаг 1: Определение принадлежности сторон треугольника
Перед тем как приступить к решению задачи, необходимо самостоятельно принять решение о том, считать ли стороны треугольника внешними или нет. На данном этапе будем считать, что область замкнутая и включает в себя свои границы. Для упрощения рассмотрим "плоский случай", однако не следует забывать и о пространственном обобщении. Поэтому типовые уравнения для прямых плоскости вида y=kx+b не будут использоваться в начале решения.
Шаг 2: Задание сторон треугольника
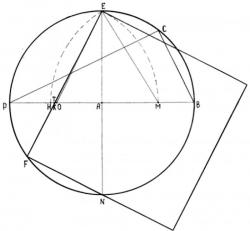
Выберите способ задания сторон треугольника. Судя по постановке задачи, это не имеет принципиального значения. Поэтому будем считать, что даны координаты его вершин A(xa, ya), B(xb, yb), C(xc, yc). Найдите направляющие векторы сторон треугольника AB={xb-xa, yb-ya}, BC={xc-xb, yc-yb}, AC={xc-xa, yc-ya} и запишите канонические уравнения прямых, содержащих эти стороны. Для AB - (x-xa)/(xb-xa)=(y-ya)/(yb-ya), для BC - (x-xb)/(xc-xb)=(y-yb)/(yc-ya), для AC - (x-xa)/(xc-xa)=(y-ya)/(yc-ya). Проведите горизонтальные и вертикальные линии в соответствии с рисунком, чтобы сократить число вычислений.
Шаг 3: Проверка принадлежности точки
Следуя вдоль оси Ox, проверьте выполнение неравенства xc ≤ xo ≤ xb. Если оно не выполняется, то точка уже находится вне пределов треугольника. Если же неравенство выполняется, то проверьте также справедливость yc ≤ yo ≤ ya. Если это неравенство не выполняется, то точка не лежит внутри треугольника. В противном случае найдите ординату прямой, содержащей AB, по формуле у1=y(xo)=[(yb-ya)(xo-xa)]/(xb-xa)+ya. Аналогично найдите ординату прямой для BC, по формуле у2=y(xo)=[(yc-yb)(xo-xb)]/(xc-xb)+yc. Составьте неравенство y2 ≤ yo ≤ y1. Если оно выполняется, то можно заключить, что заданная точка находится внутри треугольника. В противном случае точка находится вне его пределов, как показано на рисунке.