Как вычислить площадь куба
- Как вычислить площадь поверхности куба?
- Шаг 1: Вычисление площади грани
- Шаг 2: Вычисление площади поверхности
- Пример: Нахождение площади поверхности куба
- Куб и другие виды многогранников
- Советы
Как вычислить площадь поверхности куба?
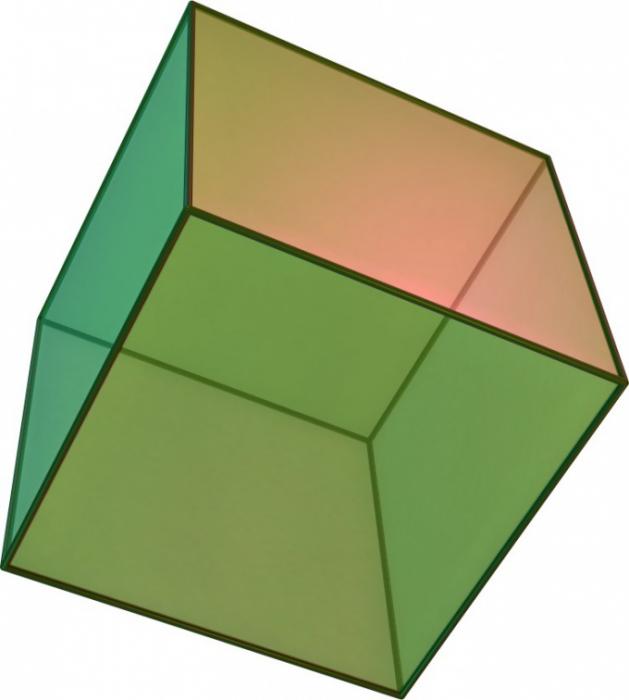
Куб - это особый вид параллелепипеда, у которого все грани являются квадратами. Узнать площадь поверхности куба несложно, если знать формулу и следовать инструкции.
Шаг 1: Вычисление площади грани
Для начала нужно вычислить площадь одной из граней куба. Площадь квадрата можно найти, перемножив длину одной из его сторон на саму себя. Это можно записать формулой: S = a*a = a².
Шаг 2: Вычисление площади поверхности
Зная площадь одной грани куба, можно найти площадь всей поверхности куба. Для этого нужно модифицировать формулу, описанную выше: S = 6*a². Это означает, что площадь поверхности куба равна площади одной грани, умноженной на 6.
Пример: Нахождение площади поверхности куба
Допустим, у нас есть куб со стороной длиной 6 см. Чтобы найти площадь поверхности куба, сначала нужно найти площадь одной грани. Подставляем значение длины стороны в формулу: S = 6*6 = 36 см². Теперь, умножая площадь грани на 6, получаем общую площадь поверхности: S = 36*6 = 216 см².
Таким образом, площадь поверхности куба со стороной длиной 6 см составляет 216 см².
Куб и другие виды многогранников
Куб является частным случаем не только параллелепипеда, но и призмы. Параллелепипед - это призма с параллелограммами в качестве оснований. У параллелепипеда 4 из 6 граней являются прямоугольниками.
Помимо куба, существуют и другие виды многогранников, такие как пирамиды, призмы, параллелепипеды и т.д. Для каждого из них существуют различные способы вычисления площадей их поверхностей.
Советы
Если у вас есть не куб, а другой правильный многогранник, то площадь его поверхности также можно вычислить по аналогичной формуле. Для этого нужно просуммировать площади всех граней, которые являются правильными многоугольниками.