Как исследовать функцию и построить ее график
- Исследование функций и построение графика
- Нахождение области определения
- Определение непрерывности и точек разрыва
- Нахождение вертикальных асимптот
- Проверка особых свойств функции
- Нахождение точек экстремума
- Определение областей монотонности
- Нахождение второй производной
- Нахождение других асимптот
- Построение графика
Исследование функций и построение графика
Исследование функций является важной частью математического анализа. Это процесс, который позволяет определить свойства функции, такие как область определения, непрерывность, асимптоты, особые свойства, точки экстремума и т. д. Построение графика функции позволяет наглядно представить ее поведение.
Нахождение области определения
Первый шаг в исследовании функции - определение области определения, то есть множества значений аргумента, при которых функция определена. Например, функция sin(x) определена на всем интервале от -∞ до +∞, а функция 1/x — на интервале от -∞ до +∞ за исключением точки x = 0.
Определение непрерывности и точек разрыва
Функция обычно непрерывна в той же области, где она определена. Для обнаружения разрывов необходимо вычислить пределы функции при приближении аргумента к изолированным точкам внутри области определения. Например, функция 1/x стремится к бесконечности, когда x→0+, и к минус бесконечности, когда x→0-. Это означает, что у нее есть разрыв второго рода в точке x = 0. Если пределы в точке разрыва конечны, но не равны, то это разрыв первого рода. Если же они равны, то функция считается непрерывной, хотя в изолированной точке она и не определена.
Нахождение вертикальных асимптот
Вертикальная асимптота практически всегда находится в точке разрыва второго рода. Иногда из области определения исключаются не отдельные точки, а целые интервалы точек, и тогда вертикальные асимптоты могут располагаться на краях этих интервалов. Найденные пределы в предыдущем шаге помогут найти вертикальные асимптоты.
Проверка особых свойств функции
Функция может обладать особыми свойствами, такими как четность, нечетность и периодичность. Четность функции означает, что для любого x в области определения f(x) = f(-x). Нечетность функции означает, что для любого x в области определения f(x) = -f(-x). Периодичность означает, что есть некое число T, называемое периодом, такое, что для любого x f(x) = f(x + T).
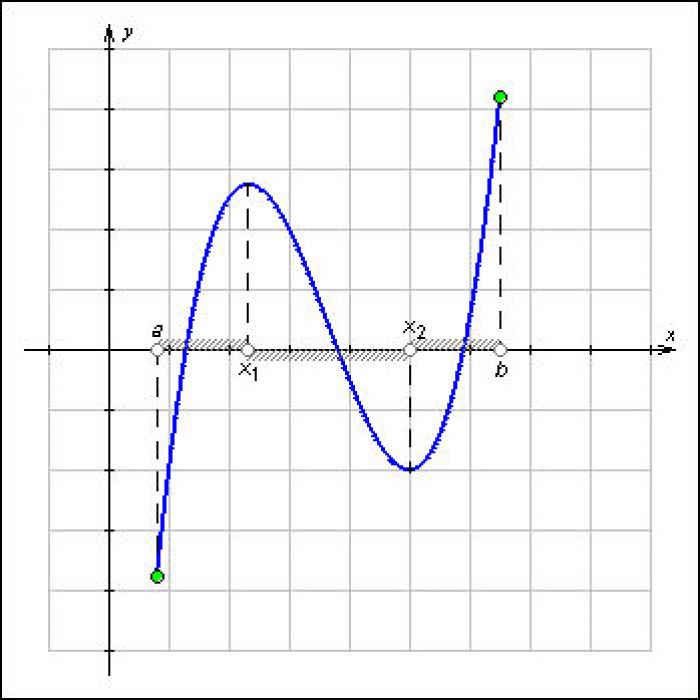
Нахождение точек экстремума
Для нахождения точек экстремума необходимо вычислить производную от функции и найти значения x, при которых она обращается в ноль. Затем следует определить, является ли каждая найденная точка максимумом или минимумом, отслеживая изменение знаков производной.
Определение областей монотонности
Области монотонности функции определяются на основе знаков производной. Функция считается монотонно возрастающей на промежутке, где производная положительна, и монотонно убывающей на промежутке, где производная отрицательна.
Нахождение второй производной
Нахождение второй производной позволяет определить выпуклость или вогнутость графика функции. Корни второй производной указывают на точки перегиба графика.
Нахождение других асимптот
Помимо вертикальных асимптот, функция может иметь и другие асимптоты, такие как горизонтальные и наклонные. Горизонтальная асимптота может быть найдена вычислением предела функции при x→∞ или x→-∞. Наклонная асимптота имеет вид прямой kx + b, где k и b находятся через вычисление пределов.
Построение графика
После проведения всех вышеуказанных шагов можно построить график функции, отметив на нем асимптоты, точки экстремума и другие важные точки. Для большей точности графика рекомендуется вычислить значения функции в нескольких промежуточных точках.
В заключение, исследование функции и построение ее графика являются важными задачами в математическом анализе. Они позволяют получить полное представление о поведении функции и выявить ее особенности. При выполнении этих задач рекомендуется использовать разработанный алгоритм и обращаться к основным свойствам элементарных функций для уточнения результатов.