Как находить стороны треугольника
- Как найти стороны треугольника
- По двум сторонам и углу между ними
- с = √(а² + b² - 2аb*cosC),
- с = √(10² + 20² - 2*10*20*cos60º) ≈ √300 ≈ 17,32.
- По двум углам и стороне
- sinA/a = sinB/b = sinC/c,
- b = 10*sin(180º-30º-20º)/sin30º ≈ 5*sin130º/0,5 ≈ 3,83.
- Ответ: длина стороны треугольника составляет примерно 3,83 см.
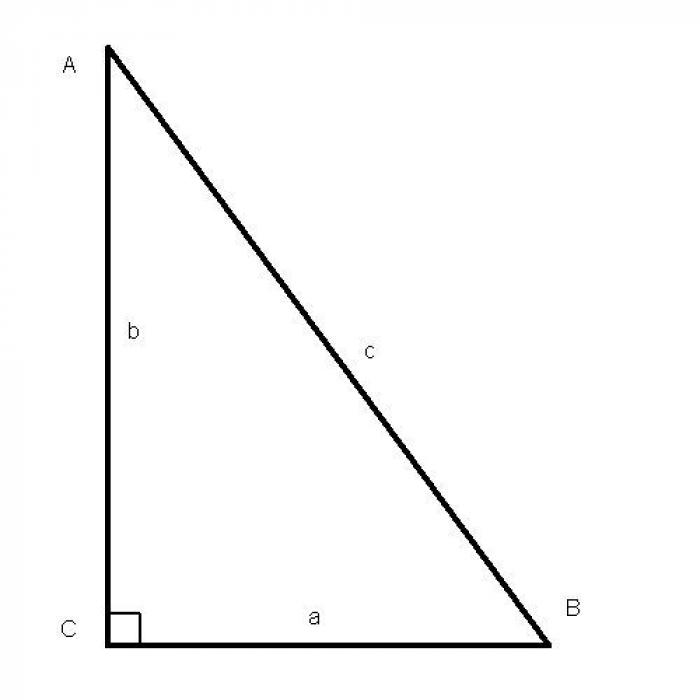
Как найти стороны треугольника
Найдение длин сторон треугольника может быть сложной задачей, особенно если известна только величина углов. Однако, с помощью соответствующих формул и теорем можно упростить этот процесс.
По двум сторонам и углу между ними
Если известны длины двух сторон треугольника и величина угла между ними, можно использовать теорему косинусов. Формула для нахождения длины третьей стороны выглядит следующим образом:
с = √(а² + b² - 2аb*cosC),
где а и b - длины известных сторон, С - величина угла между этими сторонами, с - длина искомой стороны.
Пример: Дан треугольник со сторонами 10 см и 20 см и углом между ними равным 60 градусов. Используя формулу косинусов, мы можем расчитать длину третьей стороны:
с = √(10² + 20² - 2*10*20*cos60º) ≈ √300 ≈ 17,32.
Ответ: длина стороны треугольника, противолежащей сторонам длинами 10 и 20 сантиметров и величиной угла между ними 60º, составляет около 17,32 см.
По двум углам и стороне
Если известны величины двух углов и длина одной стороны треугольника, можно использовать теорему синусов. Формула для нахождения длин двух остальных сторон выглядит следующим образом:
sinA/a = sinB/b = sinC/c,
где a, b, c - длины сторон треугольника, A, B, C - величины противолежащих углов.
Пример: Пусть в треугольнике ABC известны длина стороны а=10 см и величины углов А=30º и С=20º. Используя формулу синусов, мы можем расчитать длину стороны b: