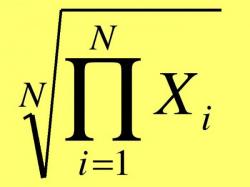Как найти базис системы

- Базисы системы векторов в линейных пространствах
- Выбор базиса линейного пространства
- Евклидово произведение векторов
- Ортогональность векторов и базис
- Разложение по ортогональному базису
- Ортогональная система функций
- Ортогональность функций в пространстве C[a,b]
Базисы системы векторов в линейных пространствах
Базисом системы векторов называют упорядоченную совокупность линейно независимых векторов e₁, e₂, …, en линейной системы X размерности n. Универсального решения задачи по нахождению базиса конкретной системы не существует. Можно сначала вычислить его, а затем доказать существование.
Выбор базиса линейного пространства
Выбор базиса линейного пространства можно осуществить при помощи второй ссылки, приведенной после статьи. Искать универсальный ответ не стоит. Подберите систему векторов, а затем приведите доказательство ее пригодности в качестве базиса. Не пробуйте делать это алгоритмически, в данном случае надо идти другим путем.
Евклидово произведение векторов
Произвольное линейное пространство, по сравнению с пространством R³, не богато свойствами. Произведите сложение или умножение вектора на число R³. Можно пойти следующим путем. Измерьте длины векторов и углы между ними. Вычислите величину площади, объемы и расстояние между объектами пространства. Затем выполните следующие манипуляции. Наложите на произвольное пространство склярное произведение векторов x и у ((x,y)=x₁y₁+x₂y₂ +…+ xnyn). Теперь его можно назвать Евклидовым. Оно представляет огромную практическую ценность.
Ортогональность векторов и базис
В произвольном по размерности базисе введите понятие ортогональности. Если склярное произведение векторов x и y равно нулю, значит они ортогональны. Такая система векторов является линейно независимой.
Разложение по ортогональному базису
Ортогональные функции в общем случае являются бесконечномерными. Поработайте с Евклидовым функциональным пространством. Разложите по ортогональному базису e₁(t), e₂(t),e₃(t), … вектора (функции) х(t). Внимательно изучите результат. Найдите коэффициент λ (координат вектора х). Для этого коэффициент Фурье умножьте на вектор еĸ (см. рисунок). Полученную в результате вычислений формулу можно назвать функциональным рядом Фурье по системе ортогональных функций.
Ортогональная система функций
Изучите систему функций 1, sint, cost, sin2t, cos2t, …, sinnt, cosnt, …. Определите ортогональна ли она на на на [-π, π]. Выполните проверку. Для этого вычислите склярные произведения векторов. Если результат проверки доказывает ортогональность этой тригонометрической системы, то она является базисом в пространстве C[-π, π].
Ортогональность функций в пространстве C[a,b]
В С[a,b] (так обозначается пространство непрерывных на [a,b] функций) скалярное произведение функций вычисляется с помощью определенного интеграла от их произведения. При этом функции ортогональны на [a,b], если ∫[a,b] φі(t)φј(t)dt=0, i≠j.
Полезный совет: Система тригонометрических функций должна быть ортогональной только именно [-π, π].