Как найти диагональ правильной призмы
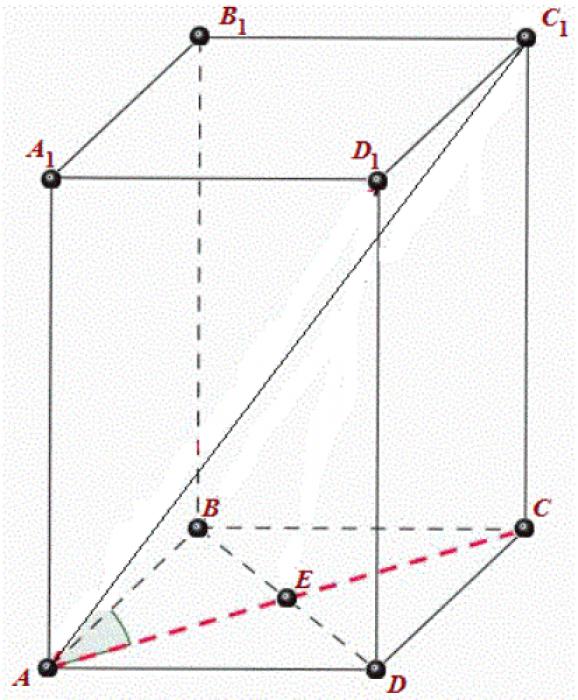
- Нахождение диагонали правильной призмы
- Определение призмы
- Определение диагонали призмы
- Нахождение диагонали призмы
- Применение теоремы Пифагора
- Рассмотрение прямоугольного треугольника
- Выражение для диагонали
Нахождение диагонали правильной призмы
Нахождение диагонали правильной призмы является важным этапом в решении различных задач. Для этого необходимо понять основные определения, связанные с призмами.
Определение призмы
Призма - это многогранник, у которого есть два равных многоугольника в качестве оснований, лежащих в параллельных плоскостях, и параллелограммы в качестве боковых граней. Прямая призма - это призма, у которой боковые грани являются прямоугольниками. А правильная призма - это прямая призма, у которой основания являются правильными многоугольниками, такими как равносторонний треугольник или квадрат.
Определение диагонали призмы
Диагональ призмы - это отрезок, соединяющий две несмежные вершины, то есть вершины, не принадлежащие одной грани.
Нахождение диагонали призмы
Для нахождения диагонали призмы можно рассмотреть треугольник, образованный этой диагональю и двумя катетами. Здесь катетами являются отрезки, соединяющие основание призмы с вершиной, принадлежащей другому основанию.
Применение теоремы Пифагора
Используя теорему Пифагора (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов), можно записать следующее уравнение:
АС₁² = АС² + СС₁²
Рассмотрение прямоугольного треугольника
Затем можно рассмотреть треугольник, образованный диагональю и одним из катетов. Для удобства можно обозначить сторону основания призмы как "а". Применяя теорему Пифагора, получим уравнение:
АС² = а² + а² = 2а²
Выражение для диагонали
Подставляя выражение для АС² в уравнение АС₁² = АС² + СС₁², получим:
АС₁ = √(2а² + h²), где а - сторона основания, h - высота призмы.
Данная формула позволяет найти диагональ любой правильной призмы.






