Как найти длину основания равнобедренного треугольника

Содержание:

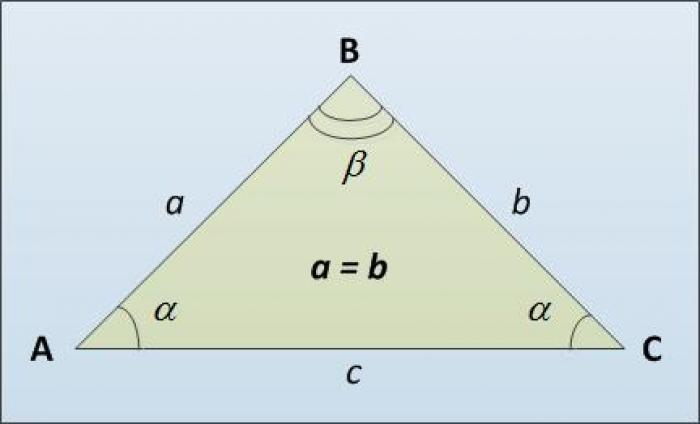
1. Основание равнобедренного треугольника
2. Вычисление основания равнобедренного треугольника
3. Альтернативный способ нахождения основания треугольника
4. Прямоугольный равнобедренный треугольник
5. Проверка результатов
6. Полезные формулы

Основание равнобедренного треугольника

Треугольник – это геометрическая фигура, которая представляет собой часть плоскости, ограниченную тремя отрезками прямых, имеющими общие концы. Стороны треугольника называются его сторонами, а их общие концы - вершинами. Если две стороны треугольника равны, то он является равнобедренным.

Вычисление основания равнобедренного треугольника

Существует несколько способов вычисления длины основания равнобедренного треугольника. Один из них - использование теоремы синусов. Согласно этой теореме, стороны треугольника пропорциональны синусам противолежащих углов. Таким образом, длина основания может быть вычислена по формуле c = a * sin β / sin α, где a - длина боковой стороны, β - угол противолежащий основанию, α - угол противолежащий боковой стороне.

Приведем пример вычисления основания треугольника с помощью теоремы синусов. Пусть a = b = 5, α = 30°. Тогда по теореме о сумме углов треугольника β = 180° - 2 * 30° = 120°. Подставляя значения в формулу, получаем c = 5 * sin 120° / sin 30° = 5 * sin 60° / sin 30° = 5 * √3 * 2 / 2 = 5 * √3.

Альтернативный способ нахождения основания треугольника

Второй способ вычисления основания треугольника - использование теоремы косинусов. Согласно этой теореме, квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенного произведения этих сторон и косинуса угла между ними. Таким образом, длина основания может быть найдена по формуле c^2 = a^2 + b^2 – 2 * a * b * cos β, где a и b - длины боковых сторон, β - угол, заключенный между этими сторонами.

Рассмотрим пример. Пусть a = b = 5, α = 30°, β = 120°. Подставляя значения в формулу, получаем c^2 = 25 + 25 - 2 * 25 * cos 120° = 50 - 50 * (- cos 60°) = 50 + 50 * ½ = 75. Извлекаем квадратный корень и получаем значение c = 5 * √3.

Прямоугольный равнобедренный треугольник

Особый случай равнобедренного треугольника - прямоугольный равнобедренный треугольник. В этом случае, основание треугольника может быть найдено с использованием теоремы Пифагора. Согласно этой теореме, квадрат длины основания равен сумме квадратов длин двух других сторон. Таким образом, длина основания может быть вычислена по формуле c = √(a^2 + b^2), где a и b - длины боковых сторон.

Проверка результатов

При вычислении длины основания равнобедренного треугольника важно быть внимательным, чтобы избежать ошибок в значениях синусов, косинусов или в арифметических действиях. Для проверки правильности результата рекомендуется вычислить длину основания двумя разными способами и сравнить полученные значения.

Полезные формулы

При вычислении угла, противолежащего основанию, удобно использовать следующие формулы приведения:
sin (180° - α) = sin α;
cos (180° - α) = - cos α.