Как найти длину стороны квадрата
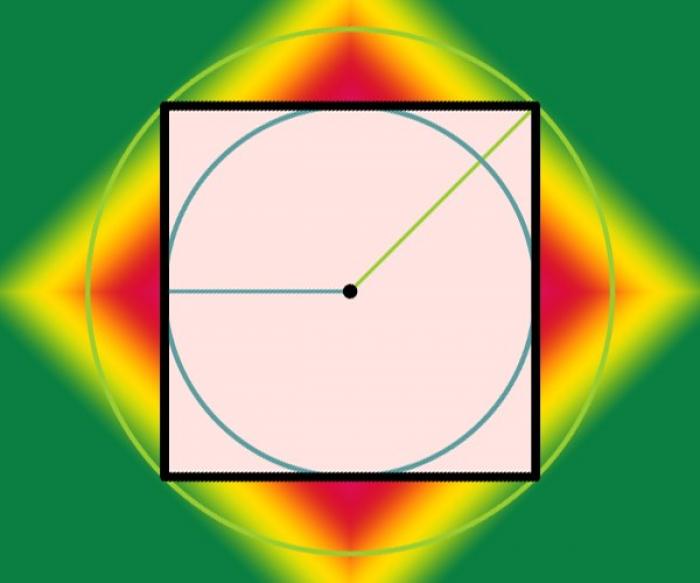
- Квадрат - одна из простейших геометрических фигур
- Вычисление длины стороны квадрата, зная периметр
- Вычисление длины стороны квадрата, зная длину диагонали
- Вычисление длины стороны квадрата, зная площадь
- Вычисление длины стороны квадрата, зная диаметр вписанной окружности
Квадрат - одна из простейших геометрических фигур
Квадрат - один из простейших плоских многоугольников правильной формы, все углы в вершинах которого равны 90°. Не так много параметров, определяющих размеры квадрата, можно назвать - это длина его стороны, длина диагонали, площадь, периметр и радиусы вписанной и описанной окружностей. Знание любого из них позволяет без проблем вычислить все остальные.
Вычисление длины стороны квадрата, зная периметр
Инструкция 1 Если вам известен периметр (Р) квадрата, то формула вычисления длины его стороны (a) будет очень проста - уменьшите эту величину в четыре раза: a = P/4. Например, при длине периметра в 100 см длина стороны должна быть равна 100/4 = 25 см.
Вычисление длины стороны квадрата, зная длину диагонали
Инструкция 2 Знание длины диагонали (l) этой фигуры тоже не особо усложнит формулу расчета длины стороны (a), но при этом придется извлекать квадратный корень из двойки. Сделав это, разделите на полученную величину известную длину диагонали: a = L/√2. Так длина диагонали в 100 см определяет длину стороны размером в 100/√2 ≈ 70,71 см.
Вычисление длины стороны квадрата, зная площадь
Инструкция 3 Заданная в условиях задачи площадь (S) такого многоугольника тоже потребует излечения корня второй степени для вычисления длины стороны (a). В этом случае извлекайте корень из единственной известной величины: a = √S. Например, площадь в 100 см² соответствует длине стороны в √100 = 10 см.
Вычисление длины стороны квадрата, зная диаметр вписанной окружности
Инструкция 4 Если в условиях задачи приведен диаметр вписанной в квадрат окружности (d), это означает, что вам досталась задача не на вычисления, а на знание определений вписанной и описанной окружностей. Численный ответ дан в условиях задачи, так как длина стороны (a) в этом случае совпадает с диаметром: a = d. А если в условиях вместо диаметра приведен радиус (r) такой окружности, увеличьте его вдвое: a = 2*r. Например, радиус вписанной окружности, равный 100 см может быть только у квадрата со стороной в 100*2 = 200 см.
Вычисление длины стороны квадрата, зная диаметр описанной около квадрата окружности
Инструкция 5 Диаметр описанной около квадрата окружности (D) совпадает с диагональю четырехугольника, поэтому используйте для вычисления длины стороны (a) формулу из второго шага, просто изменив в нем обозначение: a = D/√2. Зная радиус (R) вместо диаметра, трансформируйте эту формулу таким образом: a = 2*R/√2 = √2*R. Например, если радиус описанной окружности составляет 100 см, сторона квадрата должна быть равна √2*100 ≈ 70,71 см.