Как найти косинус, если известен синус
- Определение синуса и косинуса
- Выражение косинуса через синус
- Использование теоремы Пифагора
- Выражение косинуса через синус
- Вычисление численного значения
Определение синуса и косинуса
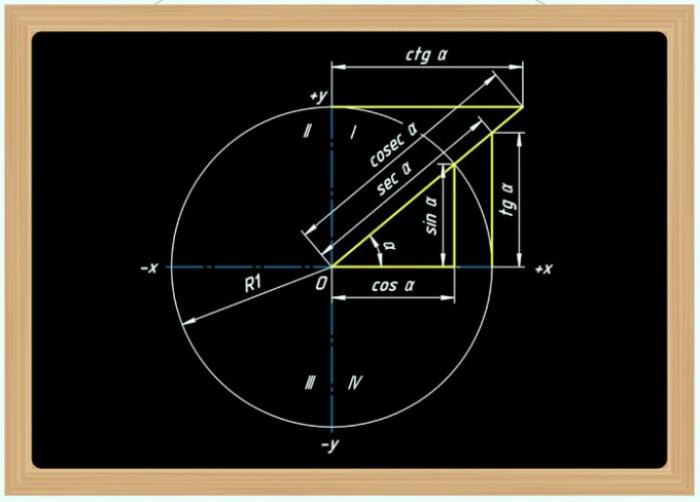
Синус и косинус - это две известные тригонометрические функции, которые могут быть определены несколькими способами - через окружность в декартовой системе координат, через решения дифференциального уравнения или через острые углы в прямоугольном треугольнике. Каждое из этих определений позволяет установить связь между синусом и косинусом.
Выражение косинуса через синус
Наиболее простой способ выразить косинус через синус - это использование определений этих функций для острых углов прямоугольного треугольника.
Сначала выражаем синус острого угла α через длины сторон прямоугольного треугольника: sin(α) = a/c, где a - длина катета, лежащего напротив угла α, и c - длина гипотенузы.
Затем находим аналогичную формулу для косинуса того же угла: cos(α) = b/c, где b - длина второго катета, примыкающего к углу α.
Использование теоремы Пифагора
Однако, чтобы получить более общую формулу, мы можем использовать теорему Пифагора для прямоугольного треугольника.
Путем деления обеих частей теоремы Пифагора на квадрат гипотенузы (a² + b² = c²) получаем следующее равенство: (a²/c² + b²/c² = 1).
Переписываем это равенство, используя выражения для косинуса и синуса: (cos²(α) + sin²(α) = 1).
Выражение косинуса через синус
Из полученного равенства выражаем косинус через синус: cos(α) = √(1 - sin²(α)).
Таким образом, мы получили общую формулу для выражения косинуса через синус.
Вычисление численного значения
Если требуется получить численный результат, можно воспользоваться калькулятором, встроенным в операционную систему Windows.
Чтобы вычислить значения тригонометрических функций, включите «инженерный» интерфейс калькулятора, нажав комбинацию клавиш Alt + 2.
Введите значение синуса угла и выполните необходимые математические операции с использованием калькулятора.






