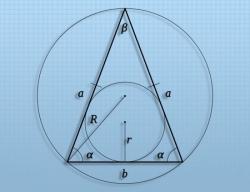
Как найти медиану равнобедренного треугольника

- Равнобедренный треугольник: особенности и вычисление медиан
- Вычисление медианы, опущенной на основание треугольника
- Вычисление медианы, проведенной к боковой стороне
Равнобедренный треугольник: особенности и вычисление медиан
Равнобедренный треугольник - это треугольник, у которого две стороны равны. Такой треугольник имеет несколько специфических свойств. Медианы, проведенные к боковым сторонам, оказываются равными. Одна медиана проводится к основанию треугольника, а вторая - к боковой стороне.
Вычисление медианы, опущенной на основание треугольника
Если у нас имеется равнобедренный треугольник ABC, и известны длины его боковой стороны и основания, мы можем легко найти медиану, опущенную на основание треугольника. Эта медиана одновременно является медианой, биссектрисой и высотой треугольника.
Мы можем воспользоваться теоремой Пифагора для прямоугольного треугольника ABD: AB² = BD² + AD², где BD - искомая медиана, AB - боковая сторона, а AD - половина основания. Таким образом, BD² = a² - b²/4. Находим корень из этого выражения и получаем длину медианы.
Вычисление медианы, проведенной к боковой стороне
Вычисление медианы, проведенной к боковой стороне, требует немного больше сложностей. Для начала, обозначим боковую сторону треугольника как a, а основание - как b. Изобразим обе медианы на рисунке. Они окажутся равными и будут делить боковую сторону на две равные части a/2.
Затем мы можем воспользоваться теоремой косинусов для треугольника AEC: AE² = AC² + CE² - 2AC·CE·cos∠ACE. Подставив известные значения, получим (3x)² = (a/2)² + b² - 2·ab/2·cosα = a²/4 + b² - ab·cosα.
Далее, применим теорему косинусов к треугольнику ABC, чтобы найти угол при основании: AB² = AC² + BC² - 2AC·BC·cos∠ACB. Раскрыв скобки, получим a² = a² + b² - 2ab·cosα. Затем выразим cosα = b/(2a) и подставим это выражение в предыдущее уравнение. Получим x² = a²/4 + b² - ab·cosα = a²/4 + b² - ab·b/(2a) = a²/4 + b² - b²/2 = (a²+2b²)/4.
Вычислив корень из правой части выражения, мы найдем медиану, проведенную к боковой стороне треугольника.