Как найти период тригонометрической функции
- Периодичность тригонометрических функций
- Определение периода простых выражений
- Период функции с углом, умноженным на число
- Период функции, возведенной в степень
- Поиск периода с использованием определения
Периодичность тригонометрических функций
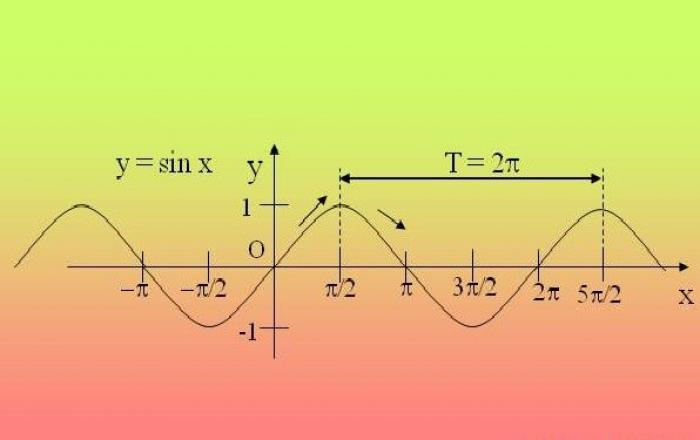
Тригонометрические функции периодичны, что означает их повторение через определенный период. Изучая функцию на данном промежутке, можно распространить найденные свойства на все остальные периоды.
Определение периода простых выражений
Если дано простое выражение, содержащее только одну тригонометрическую функцию (sin, cos, tg, ctg, sec, cosec) и угол внутри функции не умножен на число и не возведен в степень, можно использовать определение периода. Для функций sin, cos, sec, cosec период можно смело принять равным 2П, а для функций tg, ctg – П. Например, для функции у=2 sinх+5 период будет равен 2П.
Период функции с углом, умноженным на число
Если угол х под знаком тригонометрической функции умножен на число, чтобы найти период данной функции, нужно разделить стандартный период на это число. Например, для функции у=sin 5х период будет равен 2П/5.
Период функции, возведенной в степень
Чтобы найти период тригонометрической функции, возведенной в степень, нужно определить четность степени. Для четной степени стандартный период уменьшается в два раза. Например, для функции у=3 cos^2х период будет равен П. Функции tg и ctg в любой степени периодичны П.
Период функции, содержащей произведение или частное двух тригонометрических функций
Если дано уравнение, содержащее произведение или частное двух тригонометрических функций, сначала нужно найти период для каждой из них отдельно. Затем нужно найти минимальное число, которое умещает в себе целое количество обоих периодов. Например, для функции у=tgx*cos5x период будет равен 2П.
Поиск периода с использованием определения
Если затрудняетесь применять предложенные выше методы или сомневаетесь в ответе, можно действовать по определению. Возьмите в качестве периода функции Т, где Т больше нуля. Подставьте в уравнение вместо х выражение (х+Т) и решите полученное равенство, как если бы Т было параметром или числом. Таким образом, можно найти значение тригонометрической функции и подобрать минимальный период. Например, после упрощения у вас получилось тождество sin (Т/2)=0. Минимальное значение Т, при котором оно выполняется, равно 2П.






