Как найти площадь шара
- Форма шара и основные свойства
- Что такое шар и сфера?
- Шар и конус: взаимозаменяемость
- Круги и окружности на поверхности шара
- Нахождение площади шара
- Другие методы нахождения площади шара
- Заключение
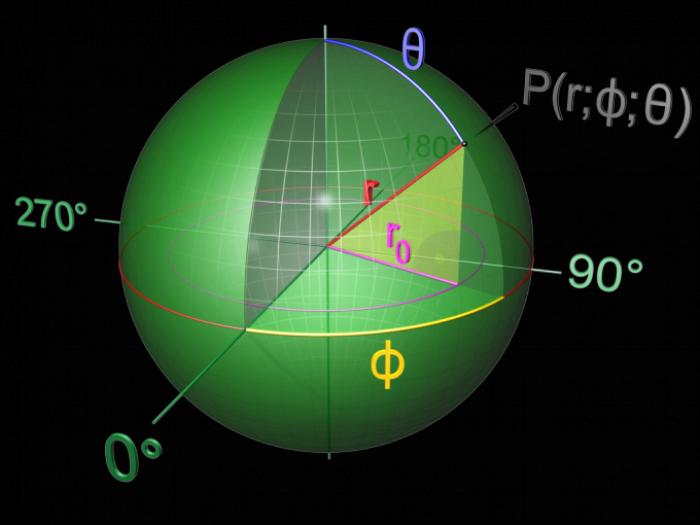
Форма шара и основные свойства
Все планеты солнечной системы и многие объекты, созданные человеком, имеют форму шара или близкую к ней. Шар имеет ось, совпадающую с диаметром, и другие важные свойства, которые мы рассмотрим.
Что такое шар и сфера?
Шаром называется тело, ограниченное сферой. Сфера, в свою очередь, представляет собой оболочку шара и является полой. Ось шара и сферы проходит через их центр, и сечения шара представляют собой круги.
Шар и конус: взаимозаменяемость
Шар и сфера являются взаимозаменяемыми телами, в отличие от конуса. При вращении сферы, сечения всегда образуют окружность, в то время как коническая поверхность получается только при вращении треугольника вдоль его оси.
Круги и окружности на поверхности шара
На поверхности шара можно провести бесконечное количество кругов или окружностей, которые проходят через две точки, расположенные в любом месте. Также, круги, проходящие через центр шара, пересекаются между собой в одном диаметре.
Нахождение площади шара
Для нахождения площади шара рассматривается площадь его сферической поверхности. Площадь сферы можно рассчитать на основании площади круга с радиусом R. Формула для нахождения площади шара: S = 4πR^2.
Другие методы нахождения площади шара
Если шар вписан в цилиндр, то можно воспользоваться теоремой Архимеда. Согласно этой теореме, площадь поверхности шара в полтора раза меньше полной поверхности цилиндра. Формула для нахождения площади шара в этом случае: S = (2/3)Sцил., где Sцил. - площадь полной поверхности цилиндра.
Заключение
Шар - одна из наиболее распространенных геометрических фигур в природе и технике. Его форма и свойства имеют важное значение при проектировании и создании различных объектов. Площадь шара может быть рассчитана на основе площади его сферической поверхности или с использованием других методов, в зависимости от задачи.