Как найти площадь треугольника
- Треугольник: основные формулы вычисления площади
- Формула площади через основание и высоту
- Формула площади через произведение сторон и синус угла
- Формула площади через вписанную окружность
- Формула площади через описанную окружность
- Формула Герона для площади треугольника
- Дополнительные формулы площади для треугольников
- Треугольники Герона
- Заключение
Треугольник: основные формулы вычисления площади
Треугольник – это простейший математический многоугольник, состоящий из трех вершин и сторон. Площадь треугольника является его основной количественной характеристикой и может быть вычислена несколькими способами на основе различных измерений, таких как длины сторон и высоты, углы между сторонами, периметр, радиусы вписанной и описанной окружности и прочее.
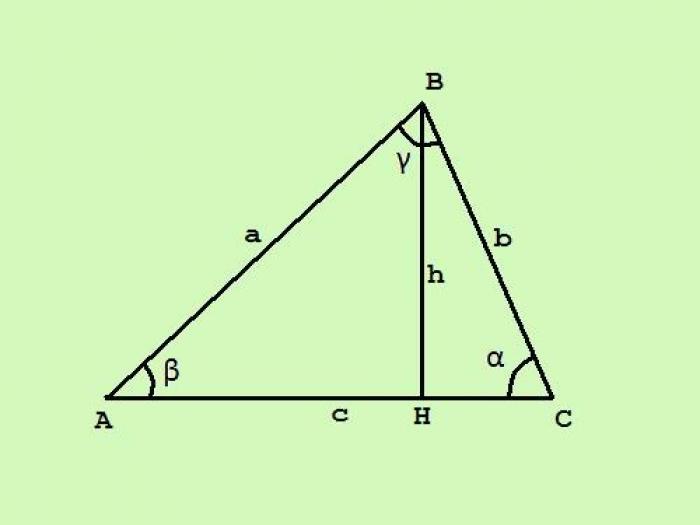
Формула площади через основание и высоту
Одним из способов вычисления площади треугольника является использование формулы, основанной на основании и высоте треугольника. Формула выглядит следующим образом: S = ?*c*h, где c – основание треугольника, h – высота, проведенная к этому основанию.
Формула площади через произведение сторон и синус угла
Другой способ вычисления площади треугольника основывается на произведении длин сторон и синусе угла между ними. Формула имеет вид: S = ?*a*b*sin?, где a и b – стороны треугольника, ? – угол между этими сторонами.
Формула площади через вписанную окружность
Если в треугольник вписана окружность радиуса r, то площадь треугольника можно вычислить с помощью следующей формулы: S = ?*P*r, где P – периметр треугольника, то есть S = ?*(a + b + c)*r.
Формула площади через описанную окружность
Если вокруг треугольника описана окружность радиуса R, то площадь треугольника может быть вычислена с использованием формулы: S = (a*b*c)/(4*R). Также существует еще одна формула, которая выражает площадь треугольника через радиус описанной окружности и углы треугольника: S = 2*R^2*sin?*sin?*sin?.
Формула Герона для площади треугольника
Существует формула Герона для вычисления площади треугольника. Она получила свое название в честь древнегреческого математика Герона Александрийского, жившего в начале нашей эры. Формула Герона выглядит следующим образом: S = ?*v((a + b + c)*(b + c - a)*(a + c - b)*(a + b - c)). Если ввести понятие полупериметра треугольника p = (a + b + c)/2, то формула упрощается до вида: S = v(p*(p - a)*(p - b)*(p - c)).
Дополнительные формулы площади для треугольников
Существуют также другие формулы для вычисления площади треугольника через длину стороны и углы треугольника, для прямоугольного треугольника, а также для равностороннего и равнобедренного прямоугольного треугольника.
Треугольники Герона
Треугольники с целочисленными сторонами, площадь которых также является целым числом, называются треугольниками Герона. Это интересное свойство делает такие треугольники особенными и привлекательными для изучения.
Заключение
Площадь треугольника может быть вычислена различными способами, в зависимости от доступных измерений. Разнообразие формул позволяет математикам и ученым проводить различные исследования и находить интересные закономерности в свойствах треугольников. Знание этих формул может быть полезным и в повседневной жизни, позволяя вычислять площадь треугольников в различных ситуациях.