Как найти пропорцию

Содержание:

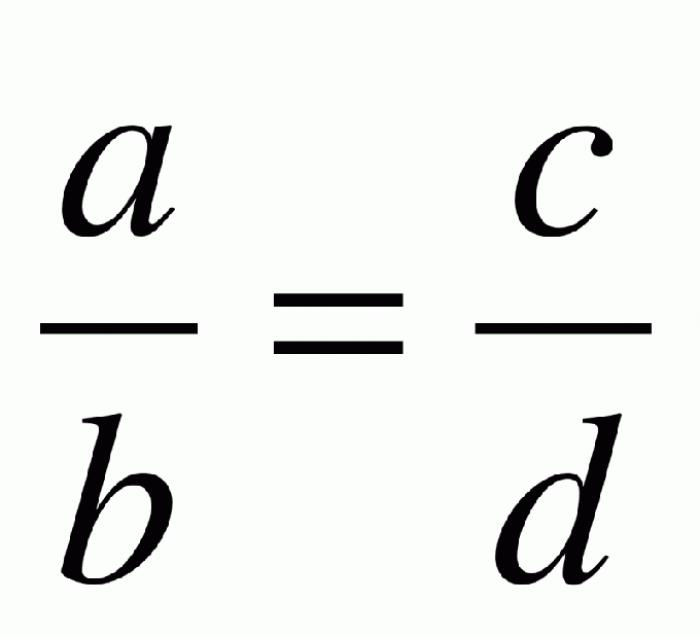
1. Пропорция в математике: основные свойства и способы решения
2. Изучение свойств пропорций
3. Решение пропорции с неизвестным членом
4. Упрощение пропорции
5. Перестановка частей пропорций
6. Решение пропорции с процентами

Пропорция в математике: основные свойства и способы решения

В математике пропорцией называется равенство двух отношений. Это взаимозависимое и неизменное соотношение, которое можно решить, используя несколько простых способов.

Изучение свойств пропорций

Прежде чем решать пропорцию, необходимо изучить ее свойства. В пропорции числа по краям равенства называются крайними, а числа, находящиеся посередине, - средними. Основное свойство пропорции заключается в том, что средние и крайние части равенства могут быть перемножены между собой. Например, в пропорции 8:4 = 6:3, если перемножить крайние части (8 * 3), получится 24, как и при умножении средних чисел. Это означает, что произведение крайних частей пропорции всегда равно произведению ее средних частей.

Решение пропорции с неизвестным членом

Чтобы вычислить неизвестный член в пропорции, нужно использовать основное свойство пропорции о равнозначности средних и крайних частей. Например, для уравнения x:4 = 8:2 мы можем записать его в виде x * 2 = 4 * 8, что равносильно x * 2 = 32. Решив это уравнение (32 / 2), мы получим недостающий член пропорции - 16.

Упрощение пропорции

Если пропорция состоит из дробных или больших чисел, ее можно упростить, разделив или умножив оба ее члена на одно и то же число. Например, пропорцию 80:20 = 120:30 можно упростить, разделив ее члены на 10 (8:2 = 12:3). Таким образом, мы получаем равнозначную пропорцию. То же самое можно сделать, увеличив все члены пропорции на одно число, например, на 2: 160:40 = 240:60.

Перестановка частей пропорций

Иногда можно переставить части пропорций, чтобы получить новые равенства. Например, в пропорции 6:10 = 24:40 мы можем поменять местами крайние части (40:10 = 24:6) или одновременно переставить все части (40:24 = 10:6). Все полученные пропорции будут равнозначными, поэтому мы можем получить несколько равенств из одной пропорции.

Решение пропорции с процентами

Для решения пропорции с процентами нужно запомнить, что проценты могут быть записаны в виде десятичной дроби. Например, пропорция 25 = 100%, 5 = x может быть решена следующим образом: мы перемножаем средние члены (5 * 100) и делим на известный крайний (25). Таким образом, мы получаем x = 20%. Точно так же можно перемножать известные крайние члены и делить их на имеющийся средний, чтобы получить искомый результат.