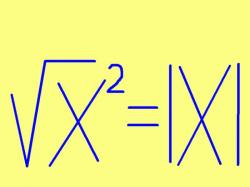Как найти сторону квадрата
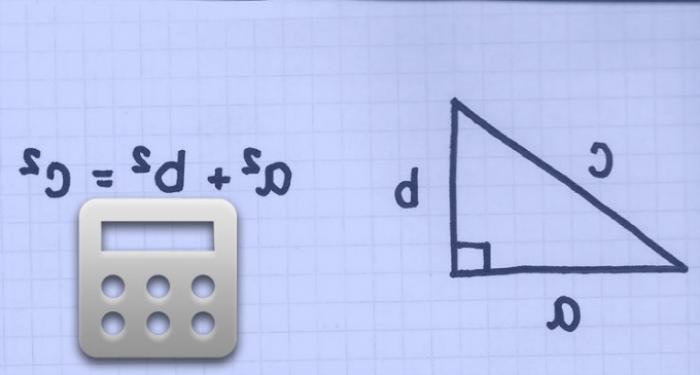
- Как найти длину стороны квадрата в геометрических задачах
- Нахождение стороны квадрата по известной площади
- Нахождение стороны квадрата по известному периметру
- Нахождение стороны квадрата по известной диагонали
Как найти длину стороны квадрата в геометрических задачах
Часто в геометрических задачах требуется найти длину стороны квадрата, если известны другие его параметры - такие, как площадь, диагональ или периметр. В этой статье мы рассмотрим несколько способов решения данной проблемы.
Нахождение стороны квадрата по известной площади
Если известна площадь квадрата, то для определения его стороны необходимо извлечь квадратный корень из числового значения площади. Формула для нахождения длины стороны выглядит следующим образом: a = √S, где a - длина стороны квадрата, S - площадь квадрата. Единицей измерения стороны квадрата будет являться линейная единица измерения длины, соответствующая единице измерения площади. Например, если площадь квадрата дана в сантиметрах квадратных, то длина его стороны будет выражена в сантиметрах.
Пример: Площадь квадрата составляет 9 квадратных метров. Найдем длину его стороны.
Решение: a = √9 = 3
Ответ: Сторона квадрата равна 3 метрам.
Нахождение стороны квадрата по известному периметру
В случае, если известен периметр квадрата, длину его стороны можно найти, разделив числовое значение периметра на четыре. Формула для нахождения длины стороны выглядит следующим образом: a = P/4, где a - длина стороны квадрата, P - периметр квадрата. Единицей измерения стороны квадрата также будет являться линейная единица измерения длины, такая же, как и у периметра. Например, если периметр квадрата задан в сантиметрах, то длина его стороны будет выражена в сантиметрах.
Пример: Периметр квадрата составляет 20 метров. Найдем длину его стороны.
Решение: a = 20/4 = 5
Ответ: Длина стороны квадрата равна 5 метрам.
Нахождение стороны квадрата по известной диагонали
Если известна длина диагонали квадрата, то длина его стороны будет равняться длине диагонали, разделенной на корень квадратный из 2. Это следует из теоремы Пифагора, так как смежные стороны квадрата и диагональ составляют прямоугольный равнобедренный треугольник. Формула для нахождения длины стороны выглядит следующим образом: a = d/√2 (т.к. a^2 + a^2 = d^2), где a - длина стороны квадрата, d - длина диагонали квадрата. Единицей измерения стороны квадрата будет такая же единица измерения длины, как и у диагонали. Например, если диагональ квадрата измерена в сантиметрах, то и длина его стороны будет выражена в сантиметрах.
Пример: Диагональ квадрата равна 10 метров. Найдем длину его стороны.
Решение: a = 10/√2, или примерно: 7,071
Ответ: Длина стороны квадрата равна 10/√2, или примерно 7,071 метра.
Теперь, когда вы знакомы с различными способами нахождения длины стороны квадрата, вы сможете успешно решать геометрические задачи, связанные с этой фигурой.