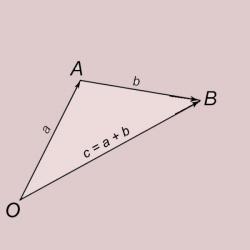
Как найти сторону треугольника, зная две стороны

- Как вычислить длину стороны треугольника
- Вычисление длины стороны при известном угле
- Вычисление длины стороны по периметру треугольника
- Вычисление длины стороны с использованием тригонометрических функций
- Вычисление длины стороны при известной площади треугольника
Как вычислить длину стороны треугольника
Вычисление длины стороны треугольника - распространенная задача, которая требует знания нескольких параметров фигуры. В этой статье мы рассмотрим различные методы для определения длины третьей стороны треугольника, основываясь на известных параметрах.
Вычисление длины стороны при известном угле
Если известно, что треугольник является прямоугольным, то это дает нам информацию о величине одного из углов, который нам нужен для вычисления третьего параметра. Если искомая сторона является гипотенузой, то мы можем использовать теорему Пифагора и вычислить ее длину по формуле C=√(A²+B²), где A и B - длины других двух сторон треугольника. Если искомая сторона является катетом, то мы можем использовать формулу C=√(A²-B²).
Вычисление длины стороны по периметру треугольника
Если мы знаем периметр треугольника (P) и длины двух известных сторон (A и B), то мы можем легко вычислить длину третьей стороны (C) путем вычитания длин известных сторон из периметра: C=P-A-B.
Вычисление длины стороны с использованием тригонометрических функций
Если мы знаем угол (γ) между двумя известными сторонами (A и B), то мы можем использовать теорему синусов для вычисления длины третьей стороны (C). Формула для вычисления стороны будет выглядеть следующим образом: C = √(A²+B²-A*B*cos(γ)), где cos(γ) - косинус угла γ.
Вычисление длины стороны при известной площади треугольника
Если мы знаем площадь треугольника (S) и длины двух известных сторон (A и B), то мы можем использовать теорему косинусов для вычисления длины третьей стороны (C). Формула для вычисления стороны будет выглядеть следующим образом: C = √(A²+B²-A*B*√(1-(2*S/(A*B))²)), где S - площадь треугольника.
В зависимости от известных параметров треугольника, вы можете выбрать подходящий метод для вычисления длины третьей стороны. Использование этих формул поможет вам справиться с задачей определения длины стороны треугольника.