Как найти точку пересечения отрезков
- Геометрические примитивы в научных и инженерных задачах
- Аппроксимация сложных объектов
- Как решить геометрическую задачу
Геометрические примитивы в научных и инженерных задачах
Простейшие геометрические примитивы, такие как точки, прямые и плоскости, являются неотъемлемой частью многих научных и инженерных задач. Они используются при проектировании, графических построениях, визуализации и машинной графике. В основе решения таких задач лежит принцип декомпозиции и последовательности элементарных действий с геометрическими примитивами.
Аппроксимация сложных объектов
В машинной графике сложные трехмерные объекты аппроксимируются полигонами, а полигоны, в свою очередь, - треугольниками. Треугольники задаются отрезками ребер, которые определяются их конечными точками. Поэтому понимание простейших геометрических задач, таких как поиск точек пересечения отрезков, является важным навыком для технических специалистов.
Как решить геометрическую задачу
Для решения геометрической задачи, например, поиска точки пересечения отрезков, вам потребуются лист бумаги и ручка. Вот инструкция:
Шаг 1: Подготовьте исходные данные
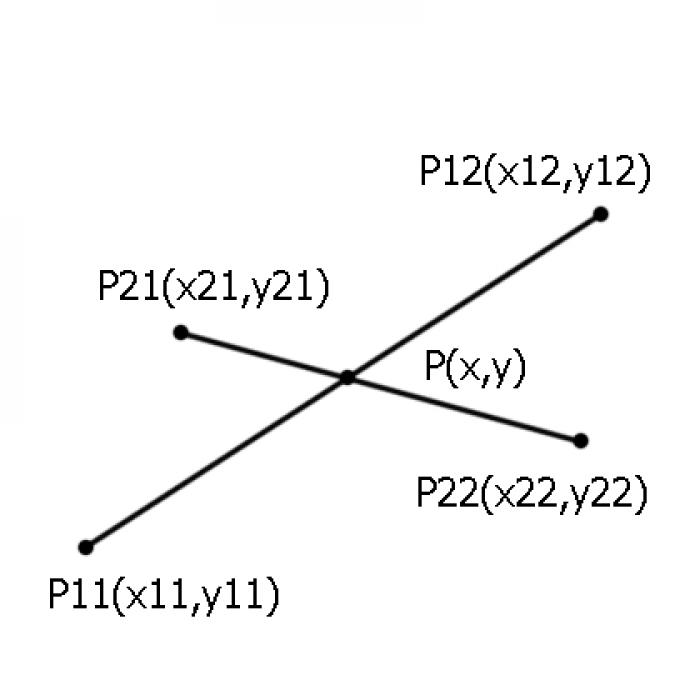
Исходные данные в данной задаче представляют собой отрезки, заданные координатами их концов в декартовой системе координат. Эта система координат имеет ортогональные оси с одинаковым линейным масштабом. Предположим, у нас есть отрезки O1 и O2, заданные точками с координатами P11(x11, y11), P12(x12, y12), P21(x21, y21) и P22(x22, y22).
Шаг 2: Составьте уравнения прямых
Уравнение прямой отрезка O1 имеет вид: K1*x+d1-y=0. Уравнение прямой отрезка O2 имеет вид: K2*x+d2-y=0. Здесь K1=(y12-y11)/(x12-x11), d1=(x12*y11-x11*y12)/(x12-x11), K2=(y22-y21)/(x22-x21), d2=(x22*y21-x21*y22)/(x22-x21).
Шаг 3: Решите систему уравнений
Решив систему уравнений, состоящую из уравнений прямых, получим значения координат точки пересечения. Вычтя из первого уравнения второе, можно получить: K1*x-K2*x+d1-d2=0. Отсюда x=(d2-d1)/(K1-K2). Подставив x в первое уравнение, получим: y=K1*(d2-d1)/(K1-K2)+d1.
Шаг 4: Проверьте результат
Чтобы убедиться, что найденная точка действительно является точкой пересечения отрезков, а не прямых, на которых они лежат, нужно проверить, что координата x принадлежит диапазонам значений [x11,x12] и [x21,x22], а координата y принадлежит диапазонам [y11,y12] и [y21,y22].
Вот и все! Теперь вы знаете, как решить простейшую геометрическую задачу - поиск точки пересечения отрезков. Этот навык будет полезен для успешного решения различных технических задач.






