Как найти третью сторону в равнобедренном треугольнике
- Равнобедренный треугольник: как найти длину основания
- Используем формулу на основе теоремы косинусов
- Обозначим известные искомые значения
- Используем формулу на основе теоремы косинусов
- По формуле, длина искомой стороны равна y√2(1-cosβ).
- Используем формулу на основе теоремы синусов
- Проверяем результат и будьте аккуратны
- Цените свой труд
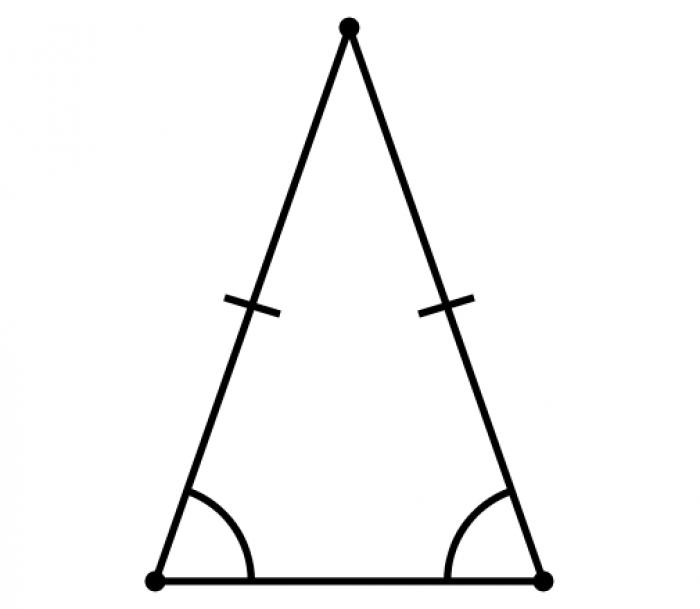
Равнобедренный треугольник: как найти длину основания
Иногда требуется найти длину основания равнобедренного треугольника, когда известны только радиусы окружностей, углы и длины боковых сторон фигуры. В данной статье мы рассмотрим несколько способов решения этой задачи.
Используем формулу на основе теоремы косинусов
Для нахождения длины основания можно воспользоваться формулой, выведенной из теоремы косинусов. Эта формула утверждает, что квадрат искомой стороны треугольника равен сумме квадратов других двух сторон, вычету удвоенного произведения этих сторон на косинус угла между ними.
Обозначим известные искомые значения
Для удобства введем следующие обозначения: α - углы, противолежащие одинаковым сторонам; β - угол между равными сторонами; R - радиус описанной окружности; r - радиус вписанной окружности. Искомую сторону обозначим как "x", а известные значения как "y".
Используем формулу на основе теоремы косинусов
По формуле, длина искомой стороны равна y√2(1-cosβ).
Используем формулу на основе теоремы синусов
Если вы не хотите использовать теорему косинусов, можно воспользоваться формулой на основе теоремы синусов. По этой формуле, длина искомой стороны равна 2ysin(β/2).
Проверяем результат и будьте аккуратны
Если результат кажется вам неправдоподобным, повторите операцию еще раз. Важно несколько раз проверить верный результат, чтобы избежать ошибок. Также будьте внимательны при оформлении решения задачи, чтобы не допустить недочетов. Мелкие ошибки могут привести к неправильному результату.
Цените свой труд
Не забывайте ценить свои усилия. Для проведения расчетов требуется немного времени. Скорее всего, вы справитесь с задачей за несколько минут.