Как найти центральный угол
- Как рассчитать центральный угол в круге?
- Рассчет центрального угла по радиусу и длине дуги
- Рассчет центрального угла по длине хорды
- Рассчет центрального угла по площади сектора
Как рассчитать центральный угол в круге?
В круге можно определить центральный угол, если известны некоторые параметры, такие как радиус, длина дуги или площадь сектора. Существуют различные формулы и методы для вычисления этого угла.
Рассчет центрального угла по радиусу и длине дуги
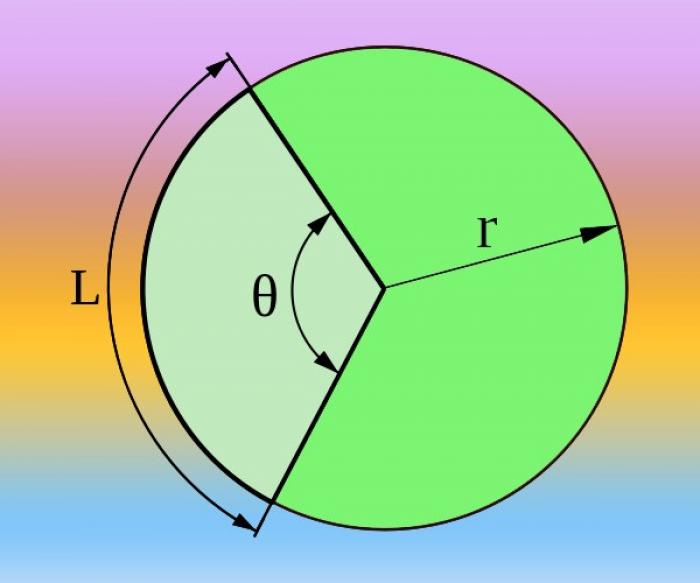
Если известны радиус круга (R) и длина дуги (L), соответствующей искомому центральному углу (θ), можно рассчитать его как в градусах, так и в радианах. Полная длина окружности равна 2*π*R, где π - математическая константа, приблизительно равная 3,14. Она соответствует центральному углу в 360° (полный оборот) или 2π радиан.
Используя пропорцию 2*π*R/L = 360°/θ = 2*π/θ, можно выразить центральный угол в радианах: θ = 2*π/(2*π*R/L) = L/R, или в градусах: θ = 360°/(2*π*R/L) = 180*L/(π*R). Подставив значения радиуса и длины дуги в формулу, можно рассчитать искомый центральный угол.
Рассчет центрального угла по длине хорды
Если известны радиус круга (R) и длина хорды (m), которая определяет центральный угол (θ), можно рассчитать его величину. Для этого можно рассмотреть равнобедренный треугольник, образованный двуми радиусами и хордой. Синус половины искомого угла равен отношению длины хорды к удвоенной длине радиуса. Используя обратную синусу функцию - арксинус, можно вычислить центральный угол: θ = 2*arcsin(½*m/R).
Рассчет центрального угла по площади сектора
Если известна площадь сектора круга (S), ограниченного радиусом (R) и центральным углом (θ), можно рассчитать величину этого угла. Удвоенное отношение площади сектора к квадрату радиуса равно центральному углу: θ = 2*S/R².
Рассчет центрального угла в долях от полного оборота или развернутого угла
Центральный угол также может быть задан в долях от полного оборота или развернутого угла. Например, для нахождения центрального угла, соответствующего четверти полного оборота, можно разделить 360° на 4: θ = 360°/4 = 90°. В радианах это значение будет равно половине полного оборота, то есть 2*π/4 ≈ 1,57.
В итоге, для рассчета центрального угла в круге можно использовать различные формулы и методы, основанные на известных значениях радиуса, длины дуги, площади сектора или доли от полного оборота.






