Как найти угол, если даны вершины треугольника
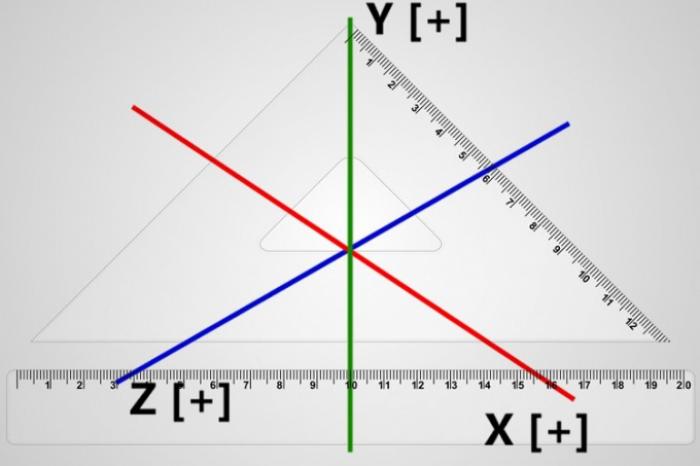
- Расчет углов в треугольнике в пространственной системе координат
- Вычисление длин сторон треугольника
- Вычисление углов треугольника
- Формула для нахождения угла треугольника по трехмерным координатам
Расчет углов в треугольнике в пространственной системе координат
Треугольник - это простейший многоугольник, для нахождения величин углов которого по известным параметрам (длинам сторон, радиусам вписанных и описанных окружностей и др.) существует несколько формул. Однако часто встречаются задачи, требующие расчета углов в вершинах треугольника, который помещен в некоторую пространственную систему координат.
Вычисление длин сторон треугольника
Если треугольник задан координатами всех трех своих вершин (X₁,Y₁,Z₁, X₂,Y₂,Z₂ и X₃,Y₃,Z₃), то начните с вычисления длин сторон, образующих тот угол треугольника (α), величина которого вас интересует. Если любую из них достроить до прямоугольного треугольника, в котором сторона будет гипотенузой, а ее проекции на две оси координат - катетами, то ее длину можно найти по теореме Пифагора. Длины проекций будут равны разности координат начала и конца стороны (т.е. двух вершин треугольника) по соответствующей оси, а значит, длину можно выразить как квадратный корень из суммы квадратов разностей таких координатных пар. Для трехмерного пространства соответствующие формулы двух сторон треугольника можно записать так: √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) и √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Вычисление углов треугольника
Используйте две формулы скалярного произведения векторов - в данном случае векторами с общим началом являются стороны треугольника, образующие вычисляемый угол. Одна из формул выражает скалярное произведение через их длины, полученные вами на предыдущем шаге, и косинус угла между ними: √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) * √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²) * cos(α). Другая - через сумму произведений координат по соответствующим осям: X₁*X₃ + Y₁*Y₃ + Z₁*Z₃.
Формула для нахождения угла треугольника по трехмерным координатам
Приравняйте эти две формулы и выразите из равенства косинус искомого угла: cos(α) = (X₁*X₃ + Y₁*Y₃ + Z₁*Z₃) / (√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) * √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²)). Тригонометрическая функция, определяющая величину угла в градусах по значению его косинуса, называется арккосинусом - используйте ее для записи окончательного варианта формулы нахождения угла по трехмерным координатам треугольника: α = arccos((X₁*X₃ + Y₁*Y₃ + Z₁*Z₃) / (√((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) * √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²))).