Как найти вторую диагональ ромба
- Ромб: основные свойства и способы рассчета диагоналей
- Известная длина одной диагонали и частный случай ромба
- Известная длина стороны и одной диагонали
- Известный угол и длина одной диагонали
- Известный периметр и длина одной диагонали
- Известная площадь и длина одной диагонали
Ромб: основные свойства и способы рассчета диагоналей
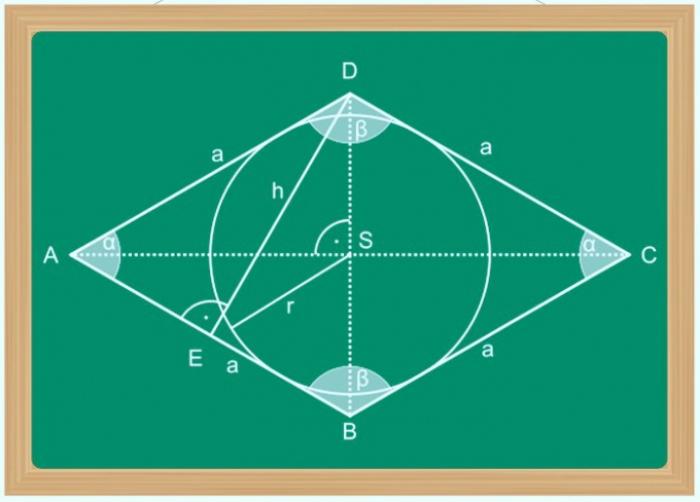
Ромб - это особый вид параллелограмма, у которого диагонали делят углы на две равные части и являются осями симметрии фигуры. Диагонали ромба пересекаются под прямым углом и имеют общую точку, которая делит каждую диагональ на две равные части. Эти свойства позволяют нам легко рассчитать длину одной из диагоналей, если известна длина другой диагонали и еще один параметр фигуры, такой как размер стороны, угол в одной из вершин или площадь.
Известная длина одной диагонали и частный случай ромба
Если мы знаем, что рассматриваемый четырехугольник является частным случаем ромба - квадратом, то нам не нужно производить никаких расчетов. В этом случае длины обеих диагоналей равны, поэтому для нахождения длины второй диагонали просто приравниваем ее к известной длине: L = l.
Известная длина стороны и одной диагонали
Если мы знаем длину стороны ромба (a) и длину одной из диагоналей (l), то мы можем рассчитать длину второй диагонали (L) с помощью теоремы Пифагора. Две половины пересекающихся диагоналей образуют прямоугольный треугольник, где половины диагоналей являются катетами, а сторона ромба - гипотенузой. Используя теорему Пифагора, мы можем записать следующее равенство: a² = (l/2)² + (L/2)². Преобразуем его для наших расчетов: L = √(4*a² - l²).
Известный угол и длина одной диагонали
Если мы знаем величину одного из углов ромба (α) и длину одной из диагоналей (l), то мы можем найти длину второй диагонали (L) с помощью тригонометрического соотношения. Рассмотрим прямоугольный треугольник, в котором тангенс половины известного угла равен отношению половины длины одной диагонали к половине длины второй диагонали: tg(α/2) = (l/2)/(L/2) = l/L. Для вычисления L используем формулу: L = l/tg(α/2).
Известный периметр и длина одной диагонали
Если нам известны длина периметра ромба (P) и длина одной из диагоналей (l), то мы можем рассчитать длину второй диагонали (L) с использованием формулы, аналогичной формуле из второго шага. Для этого мы делим периметр на четыре и заменяем длину стороны в формуле: L = √(4*(P/4)² - l²) = √(P²/4 - l²).
Известная площадь и длина одной диагонали
Если нам известна площадь ромба (S) и длина одной из диагоналей (l), то мы можем вычислить длину второй диагонали (L) используя простой алгоритм. Мы удваиваем площадь и делим полученное значение на длину известной диагонали: L = 2*S/l.
Таким образом, имея информацию о длине одной из диагоналей ромба и других параметрах фигуры, мы можем легко рассчитать длину второй диагонали. Это позволяет нам более полно изучить и понять свойства и особенности ромба.