Вам понадобитсяТрапеция представляет собой четырехугольник, две стороны которого параллельны - основания, а две другие не параллельны – боковые стороны. Трапеция, боковые стороны которой равны, называется равнобедренной или равнобочной. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований, мы рассмотрим случай, когда диагонали не перпендикулярны.
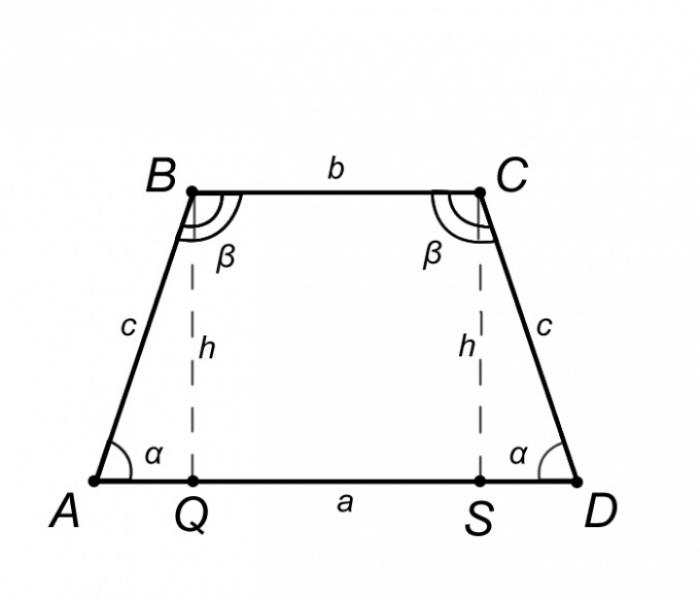
Рассмотрим равнобедренную трапецию ABCD и опишем ее свойства, но лишь те из них, знание которых поможет нам решить поставленную задачу. Из определения равнобедренной трапеции основание AD = a параллельно BC = b, а боковая сторона AB = CD = c из этого следует, что углы при основаниях равны, то есть угол BAQ = CDS = α, таким же образом угол ABC = BCD = β. Обобщив вышесказанное, справедливо утверждать, что треугольник ABQ равен треугольнику SCD, а значит, отрезок AQ = SD = (AD – BC)/2 = (a – b)/2.
Если в условии задачи нам даны длины оснований a и b, а также длина боковой стороны с, то высота трапеции h, равная отрезку BQ, находится следующим образом. Рассмотрим треугольник ABQ, так как по определению высота трапеции есть перпендикуляр к основанию, то можно утверждать, что треугольник ABQ прямоугольный. Сторона AQ треугольника ABQ, исходя из свойств равнобедренной трапеции, находится по формуле AQ = (a – b)/2. Теперь зная две стороны AQ и c, по теореме Пифагора находим высоту h. Теорема Пифагора гласит, что квадрат гипотенузы равен сумме квадратов катетов. Запишем эту теорему применительно к нашей задаче: c^2=AQ^2+ h^2. Отсюда следует, чтоh = √(c^2-AQ^2).
Для примера рассмотрим трапецию ABCD, в которой основания AD = a = 10смBC = b = 4см, боковая сторона AB = c = 12см. Найти высоту трапеции h. Находим сторону AQ треугольника ABQ.AQ = (a – b)/2 = (10-4)/2=3см. Далее подставляем значения сторон треугольника в теорему Пифагора.h = √(c^2-AQ^2) =√(12^2-3^2) =√135=11.6см.
