Как найти высоту в трапеции, если известны все стороны
- Что такое трапеция и параллелограмм?
- Как найти площадь и высоту трапеции?
- Вычисление площади треугольника ABE
- Вычисление высоты и стороны равнобедренной трапеции
- Если трапеция равнобедренная, решение можно выполнить по-другому.
- 7. Проведите из вершины C высоту CF.
Что такое трапеция и параллелограмм?
Трапецией называется выпуклый четырёхугольник, у которого параллельны две противоположные стороны и непараллельны две другие. Если все противоположные стороны четырёхугольника попарно параллельны, то это параллелограмм.
Как найти площадь и высоту трапеции?
Для вычисления площади и высоты трапеции нам понадобятся все стороны: AB, BC, CD, DA.
Вычисление площади треугольника ABE
Сначала рассмотрим решение для трапеции, которая не является равнобедренной.
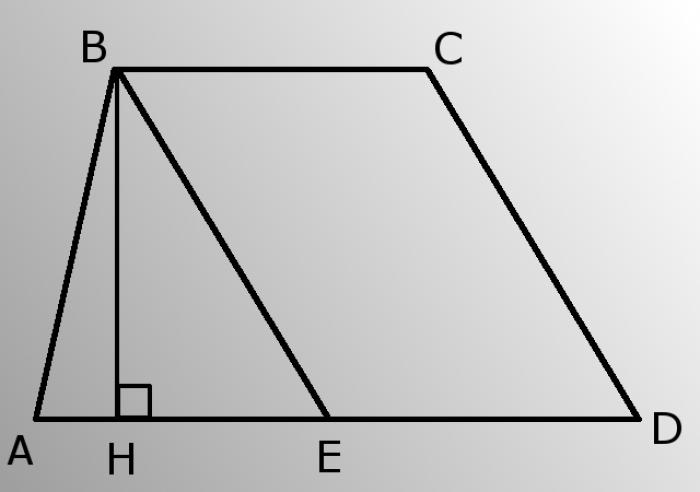
1. Проведите отрезок BE из точки B к нижнему основанию AD параллельно боковой стороне трапеции CD. Поскольку BE и CD параллельны и проведены между параллельными основаниями трапеции BC и DA, то BCDE - параллелограмм, и его противоположные стороны BE и CD равны. BE=CD.
2. Рассмотрите треугольник ABE. Вычислите сторону AE. AE=AD-ED. Основания трапеции BC и AD известны, а в параллелограмме BCDE противолежащие стороны ED и BC равны. ED=BC, значит, AE=AD-BC.
3. Теперь узнайте площадь треугольника ABE по формуле Герона, вычислив полупериметр. S=корень(p*(p-AB)*(p-BE)*(p-AE)). В этой формуле p - полупериметр треугольника ABE. p=1/2*(AB+BE+AE). Для вычисления площади вам известны все необходимые данные: AB, BE=CD, AE=AD-BC.
4. Далее запишите площадь треугольника ABE другим способом - она равна половине произведения высоты треугольника BH и стороны AE, к которой она проведена. S=1/2*BH*AE.
5. Выразите из этой формулы высоту треугольника, которая является и высотой трапеции. BH=2*S/AE. Вычислите её.
Вычисление высоты и стороны равнобедренной трапеции
Если трапеция равнобедренная, решение можно выполнить по-другому.
6. Рассмотрите треугольник ABH. Он прямоугольный, так как один из углов, BHA, прямой.
7. Проведите из вершины C высоту CF.
8. Изучите фигуру HBCF. HBCF прямоугольник, поскольку две его стороны - высоты, а другие две являются основаниями трапеции, то есть углы прямые, а противолежащие стороны параллельны. Это значит, что BC=HF.
9. Посмотрите на прямоугольные треугольники ABH и FCD. Углы при высотах BHA и CFD прямые, а углы при боковых стороных BAH и CDF равны, так как трапеция ABCD равнобедренная, значит, треугольники подобны. Так как высоты BH и CF равны или боковые стороны равнобедренной трапеции AB и CD равны, то и подобные треугольники равны. Значит, их стороны AH и FD тоже равны.
10. Найдите AH. AH+FD=AD-HF. Так как из параллелограмма HF=BC, а из треугольников AH=FD, то AH=(AD-BC)*1/2.
11. Далее из прямоугольного треугольника ABH по теореме Пифагора рассчитайте высоту BH. Квадрат гипотенузы AB равен сумме квадратов катетов AH и BH. BH=корень(AB*AB-AH*AH).






