Как научиться решать пределы
- Пределы и их последовательности: важная тема в математическом анализе
- Определение предела функции
- Простейший способ решения примеров с пределами
- Свойства пределов
- Использование "замечательных" пределов
Пределы и их последовательности: важная тема в математическом анализе
Тема "Пределы и их последовательности" является одной из ключевых в курсе математического анализа, которая является основой для изучения любых технических специальностей. Умение находить пределы функций является важным навыком для студентов высших учебных заведений.
Определение предела функции
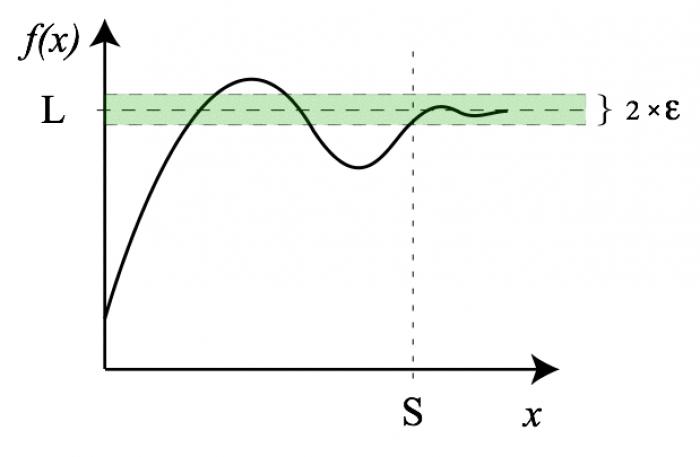
Пределом функции является число, в которое функция стремится в некоторой точке, к которой стремится аргумент. Он обозначается как lim(f(x)), где f(x) - функция, а внизу предела записывается x->x0, где x0 - число, к которому стремится аргумент.
Простейший способ решения примеров с пределами
Простейший способ решить пример с пределом - подставить вместо аргумента x в заданную функцию f(x) число x0. Если после подстановки получается конечное число, то это и будет пределом функции. Однако, если получается бесконечность, то применяются преобразования пределов.
Свойства пределов
Предел суммы равен сумме пределов, а предел произведения равен произведению пределов. Это свойство можно использовать для упрощения вычислений с пределами функций.
Использование "замечательных" пределов
Очень важно использовать так называемые "замечательные" пределы при вычислении пределов функций. Первый замечательный предел связан с тригонометрическими функциями и позволяет считать функции типа sin(x), tg(x), ctg(x) равными их аргументам x при аргументе, стремящемся к нулю. Затем, подставляя вместо аргумента x значение аргумента x0, можно получить ответ.
Второй замечательный предел часто используется при возведении суммы слагаемых, одно из которых равно единице, в степень. Доказано, что при стремлении аргумента, в которую возводится сумма, к бесконечности, функция стремится к трансцендентному числу e, приближенно равному 2,7.
Знание "замечательных" пределов и способов их преобразования является важным для успешного решения примеров с пределами функций. Оно поможет студентам развить навыки аналитического мышления и применять математические методы в решении различных задач.






