Как определить периметр прямоугольника

- Периметр прямоугольника: основные типы задач и методы их решений
- Методы решения задач на вычисление периметра прямоугольника
- Решение задачи с заданными длинами сторон
- Пример задачи с заданными длинами сторон
- Решение задачи с заданной длиной одной стороны и диагонали
- Решение задачи с заданной длиной диагонали и углом
- Решение задачи с прямоугольником, вписанным в окружность
- Решение задачи с заданной площадью прямоугольника
Периметр прямоугольника: основные типы задач и методы их решений
Периметр любого многоугольника – это сумма измерений всех его сторон. В начальном курсе геометрии часто встречаются задачи на вычисление периметра прямоугольника. Для решения таких задач иногда нужно найти длины сторон по косвенным данным. В этой статье рассмотрим основные типы задач и методы их решений.
Методы решения задач на вычисление периметра прямоугольника
Для решения задач на вычисление периметра прямоугольника вам потребуются простые инструменты: ручка и бумага для записей.
Решение задачи с заданными длинами сторон
Если известны длины всех сторон прямоугольника, периметр можно вычислить, сложив длины всех его сторон.
Формула для вычисления периметра прямоугольника: p = 2(a+b), где а и b - прилежащие стороны.
Пример задачи с заданными длинами сторон
Рассмотрим пример задачи, в которой известно, что одна сторона прямоугольника имеет длину 12 см, а вторая сторона в три раза меньше.
Для решения нужно рассчитать длину второй стороны, используя соотношение сторон прямоугольника. В данном случае, вторая сторона будет равна 12/3 = 4 см.
Теперь можно вычислить периметр прямоугольника, используя формулу: 2(4+12) = 32 см.
Решение задачи с заданной длиной одной стороны и диагонали
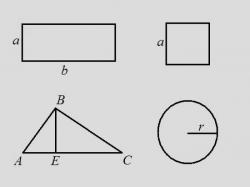
Рассмотрим задачу, в которой известна длина одной стороны прямоугольника и его диагональ. В данном случае, треугольник, образованный двумя сторонами и диагональю, является прямоугольным.
Для решения задачи, нужно найти длину второй стороны, используя уравнение Пифагора: b = (c^2-a^2)^1/2, где с - длина диагонали, а - длина известной стороны.
Затем, используя формулу для вычисления периметра прямоугольника, рассчитываем периметр.
Решение задачи с заданной длиной диагонали и углом
Еще одна задача, в которой известна длина диагонали и угол между диагональю и стороной прямоугольника. Для решения такой задачи используется следующее выражение: b = sina*c, где b - противолежащая углу сторона прямоугольника, с - его диагональ.
Также, необходимо найти прилежащую к углу сторону, используя выражение: a = cosa*c.
После нахождения длин сторон, можно определить периметр прямоугольника.
Решение задачи с прямоугольником, вписанным в окружность
Интересный случай - прямоугольник, который вписан в окружность с известным радиусом. Центр окружности совпадает с точкой пересечения диагоналей прямоугольника. Длина диагонали равна диаметру окружности.
Для решения задачи, нужно найти длины сторон прямоугольника, аналогично предыдущим методам, в зависимости от условий задачи.
Решение задачи с заданной площадью прямоугольника
Иногда в задаче известна площадь прямоугольника, а также отношение между сторонами.
Для решения такой задачи, можно обозначить длину одной стороны за x, а вторая сторона будет равна 2x. Уравнение для нахождения x будет выглядеть следующим образом: 2x*x = 32, где 32 - известная площадь.
Решив уравнение, можно найти длины сторон прямоугольника. Затем, вычисляем периметр по формуле из первого шага.
Теперь, имея основные методы решения задач на вычисление периметра прямоугольника, вы сможете успешно решать подобные задачи. Помните, что важно правильно определить известные данные и применить соответствующую формулу для решения задачи.