Как найти периметр если известна площадь
- Периметр и площадь: основные характеристики геометрических фигур
- Найдем периметр прямоугольника с заданной площадью
- В данной задаче периметр оказался равным площади фигуры.
- Нахождение периметра квадрата с заданной площадью
- Нахождение периметра треугольника с заданной площадью
- Нахождение периметра окружности с заданной площадью
Периметр и площадь: основные характеристики геометрических фигур
Площадь и периметр являются основными числовыми характеристиками любых геометрических фигур. Нахождение этих величин может быть упрощено благодаря общепринятым формулам, которые позволяют вычислить одну величину через другую с минимумом или полным отсутствием дополнительных начальных данных.
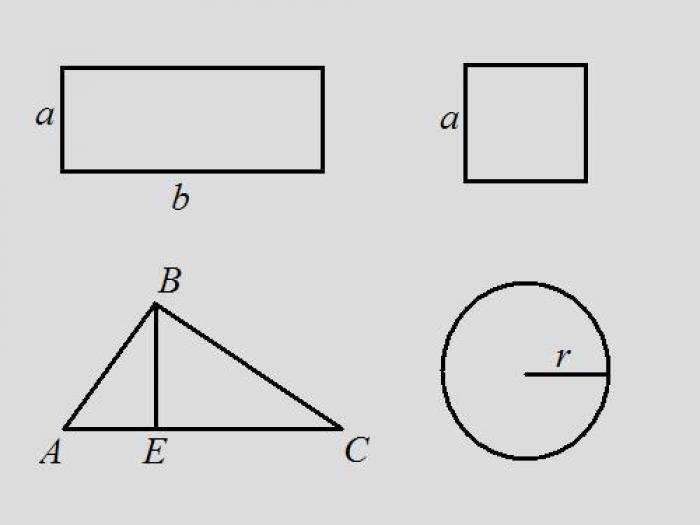
Найдем периметр прямоугольника с заданной площадью
Представим ситуацию, где известно, что площадь прямоугольника равна 18, а длина прямоугольника в 2 раза больше ширины. Периметр такого прямоугольника можно найти следующим образом:
1. Запишем формулу площади для прямоугольника - S = a*b, где a и b - длина и ширина прямоугольника соответственно.
2. Исходя из условия задачи, мы знаем, что b = 2*a. Подставим это в формулу площади: 18 = a*2*a, отсюда получаем a = √9 = 3. Очевидно, что b = 6.
3. Теперь, используя формулу периметра, найдем сумму всех сторон прямоугольника - P = 2*a + 2*b = 2*3 + 2*6 = 6 + 12 = 18.
В данной задаче периметр оказался равным площади фигуры.
Нахождение периметра квадрата с заданной площадью
Предположим, что площадь квадрата равна 9. Чтобы найти периметр, следуйте следующим шагам:
1. Используя формулу площади квадрата - S = a^2, найдем длину стороны квадрата: a = √9 = 3.
2. Так как квадрат имеет все стороны равными, периметр равен сумме длин всех сторон. Таким образом, P = 4*a = 4*3 = 12.
Нахождение периметра треугольника с заданной площадью
Допустим, у нас есть произвольный треугольник ABC, площадь которого равна 14. Если проведенная из вершины B высота делит основание треугольника на отрезки длиной 3 и 4 см, то периметр треугольника можно найти следующим образом:
1. Используя формулу для площади треугольника - S = ½*AC*BE, где AC - основание треугольника, а BE - высота, найдем длину стороны AC, сложив длины AE и EC: AC = 3 + 4 = 7.
2. Найдем высоту треугольника, используя формулу BE = S*2/AC: BE = 14*2/7 = 4.
3. Рассмотрим прямоугольный треугольник ABE. Зная катеты AE и BE, можно найти гипотенузу по формуле Пифагора: AB = √(3^2 + 4^2) = √25 = 5.
4. Рассмотрим прямоугольный треугольник BEC. По формуле Пифагора: BC = √(4^2 + 4^2) = 4*√2.
5. Таким образом, известны длины всех сторон треугольника. Найдем периметр из их суммы: P = AB + BC + AC = 5 + 4*√2 + 7 = 12 + 4*√2 = 4*(3+√2).
Нахождение периметра окружности с заданной площадью
Предположим, что площадь окружности равна 16π. Чтобы найти периметр окружности, выполните следующие действия:
1. Запишем формулу площади окружности - S = π*r^2. Найдем радиус окружности: r = √(S/π) = √16 = 4.
2. По формуле периметра окружности P = 2*π*r = 2*π*4 = 8*π. Если принять, что π = 3.14, то P = 8*3.14 = 25.12.
Таким образом, зная площадь любой геометрической фигуры, можно легко найти ее периметр, а зная периметр, можно вычислить площадь. Это позволяет упростить решение задач и облегчить работу с геометрическими фигурами.