Как построить гиперболоид
- Изучение гиперболы и гиперболоида
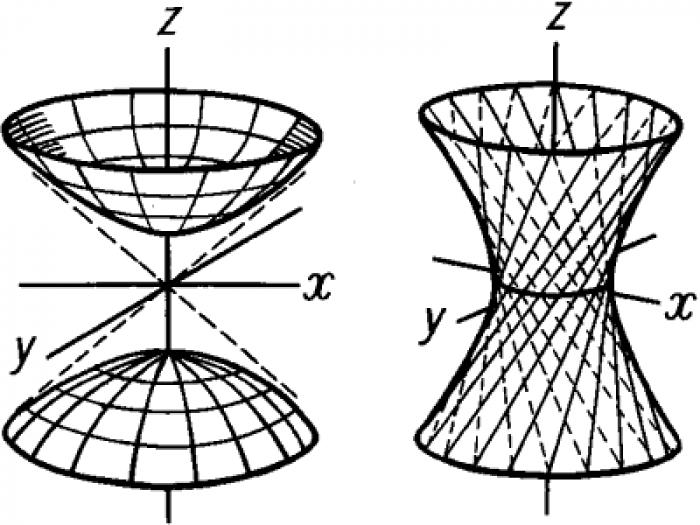
- Однополостный гиперболоид
- Сечения однополостного гиперболоида
- Построение однополостного гиперболоида
- Двуполостный гиперболоид
- Сечения двуполостного гиперболоида
- Построение двуполостного гиперболоида
Изучение гиперболы и гиперболоида
Начальные знания о гиперболе получаются в школьном курсе геометрии. В дальнейшем, изучая аналитическую геометрию в вузе, студенты узнают дополнительные сведения о гиперболе, гиперболоиде и их свойствах.
Однополостный гиперболоид
Однополостный гиперболоид - это полое тело вращения, полученное путем вращения гиперболы вокруг оси, проходящей через начало координат. Гиперболоиды бывают двух видов: однополостные и двуполостные. Однополостный гиперболоид задается уравнением x^2/a^2 + y^2/b^2 - z^2/c^2 = 1.
Сечения однополостного гиперболоида
Если рассматривать однополостный гиперболоид относительно плоскостей Oxz и Oyz, можно заметить, что его основными сечениями являются гиперболы. Однако, сечением однополостного гиперболоида плоскостью Oxy является эллипс. Самый маленький эллипс гиперболоида называется горловым эллипсом и проходит через начало координат. Уравнение горлового эллипса при z=0 записывается следующим образом: x^2/a^2 + y^2/b^2 = 1. Остальные эллипсы имеют уравнения вида: x^2/a^2 + y^2/b^2 = 1 + h^2/c^2, где h - высота однополостного гиперболоида.
Построение однополостного гиперболоида
Для построения однополостного гиперболоида начните с изображения гиперболы в плоскости Xoz. Затем постройте гиперболу в плоскости Oyz. Постройте параллелограмм в плоскости Oxy, в котором будет вписан горловой эллипс. Аналогично постройте остальные эллипсы. В результате получится чертеж однополостного гиперболоида.
Двуполостный гиперболоид
Двуполостный гиперболоид получил свое название из-за двух разных поверхностей, образованных осью Oz. Уравнение такого гиперболоида имеет вид: x^2/a^2 + y^2/b^2 - z^2/c^2 = -1.
Сечения двуполостного гиперболоида
При построении гиперболы в плоскостях Oxz и Oyz получаются эллипсы, которые являются сечениями двуполостного гиперболоида. Уравнение эллипсов имеет вид: x^2/a^2 - y^2/b^2 = h^2/c^2 - 1.
Построение двуполостного гиперболоида
Для построения двуполостного гиперболоида постройте гиперболы в плоскостях Oxz и Oyz. Затем постройте параллелограммы для построения эллипсов. Построив эллипсы, уберите все проекции построения и нарисуйте двуполостный гиперболоид.